题目内容
已知数列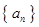 是各项均不为0的等差数列,公差为
是各项均不为0的等差数列,公差为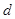 ,
,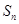 为其前n项和,且满足
为其前n项和,且满足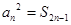 ,
,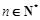 .数列
.数列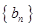 满足
满足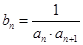 ,
,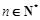 ,
, 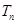 为数列
为数列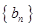 的前
的前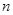 项和.
项和.
(1)求数列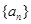 的通项公式
的通项公式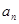 ;
;
(2)若对任意的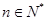 ,不等式
,不等式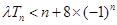 恒成立,求实数
恒成立,求实数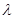 的取值范围;
的取值范围;
(3)是否存在正整数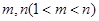 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有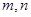
的值;若不存在,请说明理由.
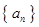 是各项均不为0的等差数列,公差为
是各项均不为0的等差数列,公差为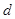 ,
,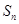 为其前n项和,且满足
为其前n项和,且满足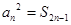 ,
,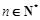 .数列
.数列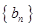 满足
满足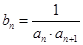 ,
,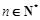 ,
, 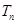 为数列
为数列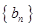 的前
的前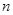 项和.
项和.(1)求数列
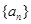 的通项公式
的通项公式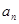 ;
;(2)若对任意的
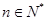 ,不等式
,不等式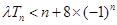 恒成立,求实数
恒成立,求实数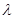 的取值范围;
的取值范围;(3)是否存在正整数
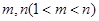 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有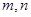
的值;若不存在,请说明理由.
(1) 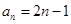 ;(2)
;(2)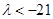 ;(3)存在,
;(3)存在,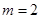 ,
, .
.
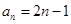 ;(2)
;(2)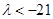 ;(3)存在,
;(3)存在,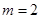 ,
, .
.试题分析:(1)利用通项公式和求和公式展开解析式,解方程组,得出
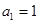 ,
,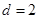 ,写出解析式;(2)先用裂项相消法求出
,写出解析式;(2)先用裂项相消法求出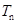 ,再讨论
,再讨论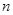 的奇数偶数两种情况,利用恒成立解题;(3)先利用等比中项列出表达式,解出
的奇数偶数两种情况,利用恒成立解题;(3)先利用等比中项列出表达式,解出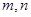 .
.试题解析:(1)在
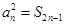 中,令
中,令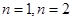 ,
,得
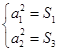 即
即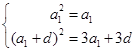 2分
2分解得
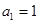 ,
,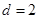 ,∴
,∴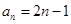 3分
3分又∵
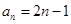 时,
时,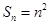 满足
满足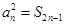 ,∴
,∴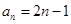 4分
4分(2)∵
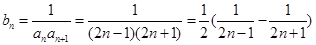 , 5分
, 5分∴
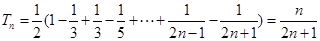 . 6分
. 6分①当
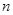 为偶数时,要使不等式
为偶数时,要使不等式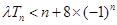 恒成立,即需不等式
恒成立,即需不等式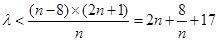 恒成立. 7分
恒成立. 7分∵
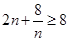 ,等号在
,等号在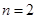 时取得.
时取得.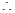 此时
此时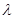 需满足
需满足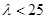 . 8分
. 8分②当
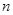 为奇数时,要使不等式
为奇数时,要使不等式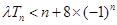 恒成立,即需不等式
恒成立,即需不等式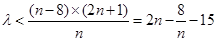 恒成立.
恒成立.∴
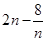 是随
是随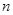 的增大而增大, ∴
的增大而增大, ∴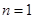 时
时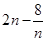 取得最小值
取得最小值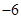 .
. 此时
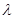 需满足
需满足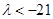 . 9分
. 9分∴综合①、②可得
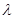 的取值范围是
的取值范围是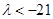 . 10分
. 10分(3)
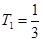 ,
,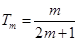 ,
,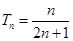 ,
, 若
 成等比数列,则
成等比数列,则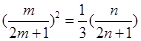 , 11分
, 11分即
 .
. 由
 ,可得
,可得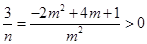 , 12分
, 12分即
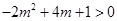 ,
,∴
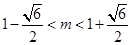 . 13分
. 13分又
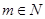 ,且
,且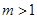 ,所以
,所以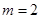 ,此时
,此时 .
.因此,当且仅当
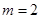 ,
, 时,数列
时,数列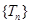 中的
中的 成等比数列. 14分
成等比数列. 14分
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 中,
中, ,
, .
. 是等比数列,并求数列
是等比数列,并求数列 ,求数列
,求数列 的前
的前 项和
项和 .
.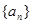 的前
的前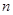 项和为
项和为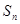 ,数列
,数列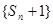 是公比为
是公比为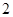 的等比数列,
的等比数列,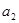 是
是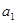 和
和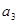 的等比中项.
的等比中项.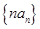 的前
的前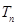 .
. 的公比
的公比 ,且
,且 成等差数列,则
成等差数列,则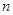 个自上而下相连的正方形着黑色或白色. 当
个自上而下相连的正方形着黑色或白色. 当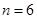 时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案如图所示. 由此推断,当
时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案如图所示. 由此推断,当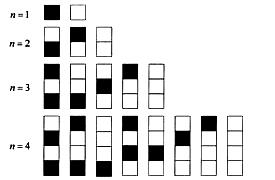
 的前
的前 项和为
项和为 ,若
,若 ,则下列式子中数值不能确定的是( )
,则下列式子中数值不能确定的是( )



 是等比数列,且
是等比数列,且 ,
, ,则
,则 的值为____.
的值为____. .
.