题目内容
给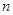 个自上而下相连的正方形着黑色或白色. 当
个自上而下相连的正方形着黑色或白色. 当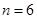 时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案如图所示. 由此推断,当
时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案如图所示. 由此推断,当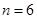 时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种. (直接用数字作答)
时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种. (直接用数字作答)
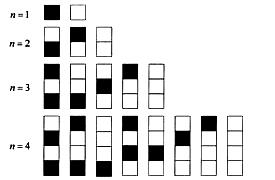
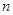 个自上而下相连的正方形着黑色或白色. 当
个自上而下相连的正方形着黑色或白色. 当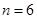 时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案如图所示. 由此推断,当
时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案如图所示. 由此推断,当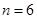 时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种. (直接用数字作答)
时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种. (直接用数字作答)
21;43
试题分析:根据题意,由于给
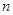 个自上而下相连的正方形着黑色或白色. 当
个自上而下相连的正方形着黑色或白色. 当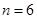 时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案规律为1,2,5,10,由此推断,依次加上7,再加9,可知当
时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案规律为1,2,5,10,由此推断,依次加上7,再加9,可知当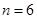 时,黑色正方形互不相邻的着色方案共有21种,至少有两个黑色正方形相邻的着色方案共有43种。故答案为21,43.
时,黑色正方形互不相邻的着色方案共有21种,至少有两个黑色正方形相邻的着色方案共有43种。故答案为21,43.点评:主要是考查了归纳推理的简单运用,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
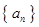 是各项均不为0的等差数列,公差为
是各项均不为0的等差数列,公差为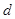 ,
,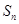 为其前n项和,且满足
为其前n项和,且满足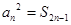 ,
,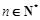 .数列
.数列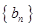 满足
满足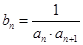 ,
,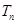 为数列
为数列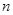 项和.
项和.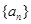 的通项公式
的通项公式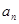 ;
;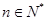 ,不等式
,不等式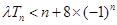 恒成立,求实数
恒成立,求实数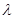 的取值范围;
的取值范围;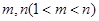 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有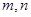
 中,
中, ,则
,则 的值是 ( )
的值是 ( ) 的各项均为正数,且
的各项均为正数,且 ,则
,则 ( )
( )
 中,公比
中,公比 ,若
,若 ,则
,则 的最值情况为
的最值情况为

 是各项均为正数的等比数列,
是各项均为正数的等比数列, ,则
,则

 是等差数列,且
是等差数列,且 ,
, .
.
 ,求数列
,求数列 的前
的前 项和.
项和. 的前
的前 项和为
项和为 ,
, ,
, ,则
,则 的值为
的值为


