题目内容

无论m取何值，函数y＝|x2－3x＋2|－m的零点个数都是

[　　]
A．

1

B．

2

C．

3

D．

不确定

答案：B
解析：

　　分析：函数y＝|x2－3x＋2|－m的零点个数就是方程|x2－3x＋2|＝m的实数根的个数，也就是函数y1＝|x2－3x＋2|与y2＝m的图象的交点个数．如下图，无论m为何值，直线y＝m恒过点P，两个函数的图象总有2个不同的交点，所以函数y＝|x2－3x＋2|－m的零点个数是2．故选B．

　　点评：解以上两个题的关键是把函数的零点或方程根的问题转化为函数图象的交点问题，利用数形结合思想求解．


练习册系列答案
相关题目
无论a取何值，函数y=ax-2（a＞0，且a≠1）的图象过定点A，而A在直线mx+ny-2=0上（m＞0，n＞0），则
2
n
+
1
m
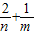的最小值为
4
4
．
无论m取何值，函数y=2sin(
kx
3
+
π
4
)在区间[m+
2
3
，m+
3
4
)(m∈R)上至少有一个最大值和最小值，则正整数k的最小值为
227
227
．
无论m取何值，函数y=2sin(
kx
3
+
π
4
)在区间[m+
2
3
，m+
3
4
)(m∈R)上至少有一个最大值和最小值，则正整数k的最小值为______．
无论a取何值，函数y=ax-2（a＞0，且a≠1）的图象过定点A，而A在直线mx+ny-2=0上（m＞0，n＞0），则的最小值为    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网