题目内容
无论m取何值，函数y=2sin(
+
)在区间[m+
，m+
)(m∈R)上至少有一个最大值和最小值，则正整数k的最小值为
| kx |
| 3 |
| π |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
227
227
．分析：先根据在任意两个整数之间（包括正整数本身）变化时，函数f（x）至少有一个最大值和最小值，可确定函数f（x）的最小正周期的范围，再由正弦函数的最小正周期的求法可得到k的取值范围，进而可得到答案．
解答：解：为使函数y=2sin(
+
)在区间[m+
，m+
)(m∈R)上至少有一个最大值和最小值，
m+
-(m+
)=
函数f（x）的最小正周期一定不大于
∴T=
=
≤
，
∴k≥72π≈72×3.14=226.8，
∴k的最小自然数为227．
| kx |
| 3 |
| π |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
m+
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 12 |
函数f（x）的最小正周期一定不大于
| 1 |
| 12 |
∴T=
| 2π | ||
|
| 6π |
| k |
| 1 |
| 12 |
∴k≥72π≈72×3.14=226.8，
∴k的最小自然数为227．
点评：本题主要考查正弦函数的基本性质--周期性．三角函数是高考的一个重要考点，属于中档题．
练习册系列答案
相关题目
的零点个数都是
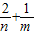的最小值为 ．