题目内容
在边长为a的等边三角形ABC中，AD⊥BC于D，沿AD折成二面角B-AD-C后，
，这时二面角B-AD-C的大小为 ．
【答案】分析：根据已知中AD⊥BC于D，易得沿AD折成二面角B-AD-C后，∠BDC即为二面角B-AD-C的平面角，解三角形BDC即可求出二面角B-AD-C的大小．
解答：解：∵AD⊥BC
∴沿AD折成二面角B-AD-C后，
AD⊥BD，AD⊥CD
故∠BDC即为二面角B-AD-C的平面角
又∵BD=CD=
，
∴∠BDC=60°
故答案为：60°
点评：本题考查的知识点是二面角的平面角的求法，解答的关键是求出二面角的平面角，将问题转化为一个解三角形问题．
解答：解：∵AD⊥BC
∴沿AD折成二面角B-AD-C后，
AD⊥BD，AD⊥CD
故∠BDC即为二面角B-AD-C的平面角
又∵BD=CD=
，∴∠BDC=60°
故答案为：60°
点评：本题考查的知识点是二面角的平面角的求法，解答的关键是求出二面角的平面角，将问题转化为一个解三角形问题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
在三棱锥P-ABC中，△PAC和△PBC是边长为
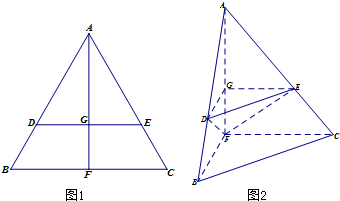（2013•广东）如图1，在边长为1的等边三角形ABC中，D，E分别是AB，AC边上的点，AD=AE，F是BC的中点，AF与DE交于点G，将△ABF沿AF折起，得到如图2所示的三棱锥A-BCF，其中