题目内容
已知函数![]() R
R![]() ,
, ![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的方程
的方程![]()
![]() 为自然对数的底数)只有一个实数根,求
为自然对数的底数)只有一个实数根,求![]() 的值。
的值。
已知函数![]() R
R![]() ,
, ![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的方程
的方程![]()
![]() 为自然对数的底数)只有一个实数根,求
为自然对数的底数)只有一个实数根,求![]() 的值。
的值。
解: 函数![]() 的定义域为
的定义域为![]() .
.
∴![]()
![]() .
.
① 当![]() , 即
, 即![]() 时, 得
时, 得![]() ,则
,则![]() . ∴
. ∴![]() 在
在![]() 上单调递增.
上单调递增.
② 当![]() , 即
, 即![]() 时, 令
时, 令![]() 得
得![]() ,
,
解得![]() .
.
(ⅰ) 若![]() , 则
, 则![]() .
.
∵![]() , ∴
, ∴![]() , ∴函数
, ∴函数![]() 在
在![]() 上单调递增.分
上单调递增.分
(ⅱ)若![]() ,则
,则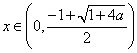 时,
时, ![]() ;
; 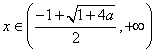 时,
时, ![]() ,∴函数
,∴函数![]() 在
在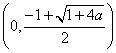 上单调递减, 在
上单调递减, 在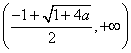 上单调递增. , 综上所述, 当
上单调递增. , 综上所述, 当![]() 时, 函数
时, 函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,
时, ![]() 的递减区间为
的递减区间为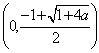 , 递增区间为
, 递增区间为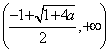 .
.
(2) 解: 令![]() , 则
, 则![]() .令
.令![]() , 得
, 得![]() . ks5u
. ks5u
当![]() 时,
时, ![]() ; 当
; 当![]() 时,
时, ![]() .ks5u
.ks5u
∴函数![]() 在区间
在区间![]() 上单调递增, 在区间
上单调递增, 在区间![]() 上单调递减.
上单调递减.
∴当![]() 时, 函数
时, 函数![]() 取得最大值, 其值为
取得最大值, 其值为![]() .
.
而函数![]() ,
,
当![]() 时, 函数
时, 函数![]() 取得最小值, 其值为
取得最小值, 其值为![]() .
.
∴ 当![]() , 即
, 即![]() 时, 方程
时, 方程![]() 只有一个根.
只有一个根.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
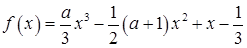 (
(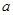
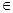 R).
R).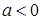 ,求函数
,求函数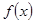 的极值;
的极值;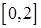 上有两个零点,若存在,求出
上有两个零点,若存在,求出 R
R ,
,  .
. 的单调区间;
的单调区间; 的方程
的方程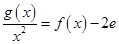
 为自然对数的底数)只有一个实数根, 求
为自然对数的底数)只有一个实数根, 求 的值.
的值.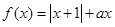 (
(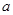 ∈R).
∈R).