题目内容
已知椭圆 的面积为πab,设平面区域
的面积为πab,设平面区域 .
.(Ⅰ)求平面区域M的面积;
(Ⅱ)若动直线x=t被平面区域M截得的线段长为d,试用t表示d并求出d的最大值.
【答案】分析:(I)由题意可得:平面区域M如图中阴影部分,则它的面积为此椭圆面积的 再减去△OAB的面积,结合题中的条件计算出各部分的面积进而达到答案.
再减去△OAB的面积,结合题中的条件计算出各部分的面积进而达到答案.
(II)直线x=t在平面区域M中截得的线段长 ,再利用三角换元的有关知识与三角函数的有关性质求出最大值即可.
,再利用三角换元的有关知识与三角函数的有关性质求出最大值即可.
解答: 解:(I)由题意可得:平面区域M如图中阴影部分,则它的面积为此椭圆面积的
解:(I)由题意可得:平面区域M如图中阴影部分,则它的面积为此椭圆面积的 再减去△OAB的面积,---(3分)
再减去△OAB的面积,---(3分)
由题中的条件可得:椭圆面积的 为
为 ,三角形OAB的面积为1,
,三角形OAB的面积为1,
所以阴影部分的面积为 ;---(6分)
;---(6分)
(II)直线x=t在平面区域M中截得的线段长 ,---(10分)
,---(10分)
设 ,
,
则有
根据三角函数的性质可得:当 时,
时, .---(14分)
.---(14分)
点评:解决此类问题的关键是熟练掌握三角换元与三角函数的有关性质,以及椭圆的标准方程与性质,此题属于中档题.
 再减去△OAB的面积,结合题中的条件计算出各部分的面积进而达到答案.
再减去△OAB的面积,结合题中的条件计算出各部分的面积进而达到答案.(II)直线x=t在平面区域M中截得的线段长
 ,再利用三角换元的有关知识与三角函数的有关性质求出最大值即可.
,再利用三角换元的有关知识与三角函数的有关性质求出最大值即可.解答:
 解:(I)由题意可得:平面区域M如图中阴影部分,则它的面积为此椭圆面积的
解:(I)由题意可得:平面区域M如图中阴影部分,则它的面积为此椭圆面积的 再减去△OAB的面积,---(3分)
再减去△OAB的面积,---(3分)由题中的条件可得:椭圆面积的
 为
为 ,三角形OAB的面积为1,
,三角形OAB的面积为1,所以阴影部分的面积为
 ;---(6分)
;---(6分)(II)直线x=t在平面区域M中截得的线段长
 ,---(10分)
,---(10分)设
 ,
,则有

根据三角函数的性质可得:当
 时,
时, .---(14分)
.---(14分)点评:解决此类问题的关键是熟练掌握三角换元与三角函数的有关性质,以及椭圆的标准方程与性质,此题属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
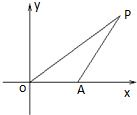 如图,已知△OAP的面积为S,
如图,已知△OAP的面积为S, (2012•安徽)如图,F1、F2分别是椭圆C:
(2012•安徽)如图,F1、F2分别是椭圆C: +
+ =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°
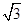 ,求a,b的值
,求a,b的值