Question

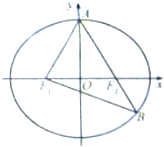
（2012•安徽）如图，F₁、F₂分别是椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的左、右焦点，A是椭圆C的顶点，B是直线AF₂与椭圆C的另一个交点，∠F₁AF₂=60°．
（Ⅰ）求椭圆C的离心率；
（Ⅱ）已知△AF₁B的面积为40

3

，求a，b 的值．

Answer 1

分析：（Ⅰ）直接利用∠F₁AF₂=60°，求椭圆C的离心率；
（Ⅱ）设|BF₂|=m，则|BF₁|=2a-m，利用余弦定理以及已知△AF₁B的面积为40

3

，直接求a，b 的值．

解答：解：（Ⅰ）∠F₁AF₂=60°?a=2c?e=

c

a

=

1

2

．
（Ⅱ）设|BF₂|=m，则|BF₁|=2a-m，
在三角形BF₁F₂中，|BF₁|²=|BF₂|²+|F₁F₂|²-2|BF₂||F₁F₂|cos120°
?（2a-m）²=m²+a²+am．?m=

3

5

a．
△AF₁B面积S=

1

2

|BA||F₁A|sin60°
?

1

2

×a×(a+

3

5

a) ×

3

2

=40

3

?a=10，
∴c=5，b=5

3

．

点评：本题考查椭圆的简单性质，余弦定理的应用，考查计算能力．