Question

已知向量

a

=（sinx，2cosx），

b

=（2sinx，sinx），函数f（x）=

a

•

b

-1．
（1）求函数f（x）的最小正周期和最大值；
（2）在给出的直角坐标系中，画出f（x）在区间[0，π]上的图象．

Answer 1

分析：（1）根据所给的两个向量的坐标和函数的表示式，根据两个向量的数量积的坐标形式写出三角函数式，利用幅角公式写出最简形式，求出周期和最大值．
（2）先列表，再在直角坐标系中画出函数y=f（x）在区间[0，π]上的图象．

解答：解：（1）f（x）=2sin²x+2sin xcos x-1=sin 2x-cos 2x=

2

sin（2x-

π

4

）
∴T=

2π

2

=π，…（3分）
当2x-

π

4

=2kπ+

π

2

，即x=kπ+

3π

8

 （k∈Z）时，函数f（x）取得最大值

2

．…（6分）
（2）列表：

2x- π 4	- π 4	0	π 2	π	3π 2	7π 4
x	0	π 8	3π 8	5π 8	7π 8	π
y	-1	0	2	0	- 2	-1

…（9分）
描点连线，得函数图象如图所示：

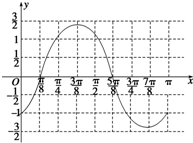
…（12分）

点评：本题考查三角函数的性质，是一个以向量为载体的题目，这种题目经常出现在高考卷中，是一个典型的三角函数解答题目．