题目内容
已知函数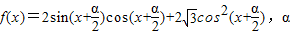 为常数
为常数(1)求f(x)的最小正周期.
(2)若0≤α≤π,求使f(x)为偶函数的α的值.
【答案】分析:(1)f(x)=sin(2x+α)+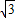 cos(2x+α)+
cos(2x+α)+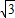 =2sin(2x+α+
=2sin(2x+α+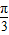 )+
)+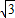 ,最小正周期为
,最小正周期为 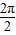 =π.
=π.
(2)要使f(x)=2sin(2x+α+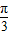 )+
)+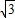 为偶函数,α+
为偶函数,α+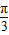 =kπ+
=kπ+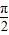 ,k∈z,根据α的范围,求出α的大小.
,k∈z,根据α的范围,求出α的大小.
解答:解:(1)f(x)=sin(2x+α)+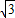 cos(2x+α)+
cos(2x+α)+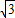 =2sin(2x+α+
=2sin(2x+α+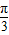 )+
)+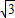 ,
,
故最小正周期为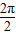 =π.
=π.
(2)若0≤α≤π,要使f(x)=2sin(2x+α+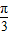 )+
)+ 为偶函数,α+
为偶函数,α+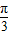 =kπ+
=kπ+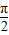 ,k∈z,
,k∈z,
∴α=kπ+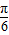 ,再根据0≤α≤π,可得 α=
,再根据0≤α≤π,可得 α=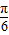 .
.
点评:本题考查两角和正弦公式,正弦函数的周期性、奇偶性,求出f(x)的解析式为2sin(2x+α+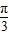 )+
)+ ,是解题的关键.
,是解题的关键.
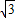 cos(2x+α)+
cos(2x+α)+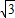 =2sin(2x+α+
=2sin(2x+α+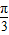 )+
)+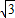 ,最小正周期为
,最小正周期为 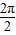 =π.
=π.(2)要使f(x)=2sin(2x+α+
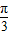 )+
)+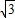 为偶函数,α+
为偶函数,α+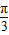 =kπ+
=kπ+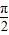 ,k∈z,根据α的范围,求出α的大小.
,k∈z,根据α的范围,求出α的大小.解答:解:(1)f(x)=sin(2x+α)+
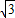 cos(2x+α)+
cos(2x+α)+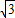 =2sin(2x+α+
=2sin(2x+α+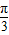 )+
)+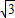 ,
,故最小正周期为
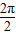 =π.
=π.(2)若0≤α≤π,要使f(x)=2sin(2x+α+
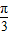 )+
)+ 为偶函数,α+
为偶函数,α+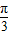 =kπ+
=kπ+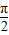 ,k∈z,
,k∈z,∴α=kπ+
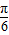 ,再根据0≤α≤π,可得 α=
,再根据0≤α≤π,可得 α=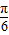 .
.点评:本题考查两角和正弦公式,正弦函数的周期性、奇偶性,求出f(x)的解析式为2sin(2x+α+
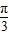 )+
)+ ,是解题的关键.
,是解题的关键. 
练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
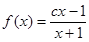 (
(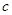 为常数).
为常数).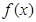 的零点, 求
的零点, 求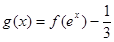 , 求函数
, 求函数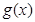 的零点.
的零点. .(
.( 为常数)
为常数) 时,求函数
时,求函数 的最小值;
的最小值; 上的最值;
上的最值; 都有
都有