题目内容
10.求满足下列条件的函数f(x).(1)f(x)是三次函数,且f(0)=3,f′(0)=0,f′(1)=-3,f′(2)=0;
(2)f′(x)是一次函数,x2f′(x)-(2x-1)f(x)=1.
分析 (1)设出函数解析式f(x)=ax3+bx2+cx+d(a≠0),由f(0)=3求得d,再求出导函数,结合f′(0)=0,f′(1)=-3,f′(2)=0列式求得a,b,c的值,则函数解析式可求;
(2)由f′(x)是-次函数,可设f′(x)=ax+b(a≠0),求出其原函数,代入x2f′(x)-(2x-1)f(x)=1,整理后比较系数列式求得a,b,c的值,则答案可求.
解答 解:(1)设f(x)=ax3+bx2+cx+d(a≠0),
∵f(0)=3,∴d=3,
∴f(x)=ax3+bx2+cx+3,f′(x)=3ax2+2bx+c,
由f′(0)=0,f′(1)=-3,f′(2)=0,得
$\left\{\begin{array}{l}{c=0}\\{3a+2b+c=-3}\\{12a+4b+c=0}\end{array}\right.$,解得a=1,b=-3,c=0.
∴f(x)=x3-3x2+3;
(2)∵f′(x)是-次函数,
∴可设f′(x)=ax+b(a≠0),
则f(x)=$\frac{1}{2}a{x}^{2}+bx+c$(a≠0),
由x2f′(x)-(2x-1)f(x)=1,得
${x}^{2}(ax+b)-(2x-1)(\frac{1}{2}a{x}^{2}+bx+c)-1=0$,
即$(\frac{1}{2}a-b){x}^{2}-(2c-b)x+c-1=0$.
∴$\left\{\begin{array}{l}{\frac{1}{2}a-b=0}\\{2c-b=0}\\{c-1=0}\end{array}\right.$,解得a=4,b=2,c=1.
∴f(x)=2x2+2x+1.
点评 本题考查导数的运算,考查了利用待定系数法求函数解析式,是基础题.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案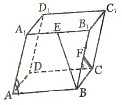 已知平行六面体ABCD-A1B1C1D1的所有棱长都是1,且∠A1AB=∠A1AD=∠BAD=60°,E、F分别为A1B1与BB1的中点,求异面直线BE与CF所成的角.
已知平行六面体ABCD-A1B1C1D1的所有棱长都是1,且∠A1AB=∠A1AD=∠BAD=60°,E、F分别为A1B1与BB1的中点,求异面直线BE与CF所成的角.