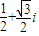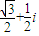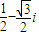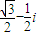题目内容
已知 =(cos23°,cos67°),
=(cos23°,cos67°), =(2cos68°,2cos22°),则△ABC的面积为________.
=(2cos68°,2cos22°),则△ABC的面积为________.

分析:根据题意,利用
 、
、 的坐标,可得
的坐标,可得 、
、 的模,由数量积公式,可得
的模,由数量积公式,可得 •
• 的值,进而由cos∠B=
的值,进而由cos∠B=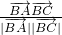 ,可得cos∠B,由余弦函数的性质,可得∠B,最后由三角形面积公式,计算可得答案.
,可得cos∠B,由余弦函数的性质,可得∠B,最后由三角形面积公式,计算可得答案.解答:根据题意,
 =(cos23°,cos67°),则
=(cos23°,cos67°),则 =-(cos23°,sin23°),有|
=-(cos23°,sin23°),有| |=1,
|=1, =(2cos68°,2cos22°)=2(cos68°,sin68°),则|
=(2cos68°,2cos22°)=2(cos68°,sin68°),则| |=2,
|=2,则
 •
• =-2(cos23°cos68°-sin23°sin68°)=-2×cos45°=-
=-2(cos23°cos68°-sin23°sin68°)=-2×cos45°=- ,
,cos∠B=
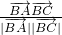 =-
=- ,
,则∠B=135°,
则S△ABC=
 |
| |•|
|•| |sin∠B=
|sin∠B= ×1×2×
×1×2× =
= ;
;故答案为
 .
.点评:本题考查数量积的坐标运算,关键是由余弦函数的和角公式求出
 •
• ,注意角B是向量
,注意角B是向量 、
、 的夹角.
的夹角. 
练习册系列答案
相关题目