题目内容
已知向量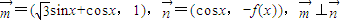 .
.(1)求f(x)的单调区间;
(2)已知A为△ABC的内角,若
 ,求△ABC的面积.
,求△ABC的面积.
【答案】分析:(1)通过向量的垂直,推出f(x)的表达式,利用二倍角公式以及两角和的正弦函数化简,然后求解函数的单调区间;
(2)通过 ,A为△ABC的内角,求出A,利用正弦定理求出B,三角形的两角和求出C,通过
,A为△ABC的内角,求出A,利用正弦定理求出B,三角形的两角和求出C,通过 ,求△ABC的面积.
,求△ABC的面积.
解答:解:(1)因为向量 .
.
∴f(x)= sinxcosx+cos2x=
sinxcosx+cos2x= +
+ =sin(2x+
=sin(2x+ )+
)+ ,
,
∴f(x)的单调增区间为:[ ],k∈Z.
],k∈Z.
函数的单调减区间为 ,k∈Z.
,k∈Z.
(2)由 ,所以
,所以 ,
,
∴sin(A+ )=
)= ,
,
∵A是三角形内角,∴A+ ∈(
∈( ),∴A=
),∴A= 或A=
或A= ,
,
又 ,∴A=
,∴A= ,
,
由正弦定理可得sinB= =
= ,⇒B=
,⇒B= 或
或 ,
,
C=π-A-B= 或
或
所以△ABC的面积为: =
= =
= ,
,
或 =
= =
= .
.
点评:本题考查向量的数量积两角和的正弦函数的应用,正弦定理,正弦函数的单调性,三角形的面积的求法,考查计算能力,转化思想的应用,分类讨论思想的应用.
(2)通过
 ,A为△ABC的内角,求出A,利用正弦定理求出B,三角形的两角和求出C,通过
,A为△ABC的内角,求出A,利用正弦定理求出B,三角形的两角和求出C,通过 ,求△ABC的面积.
,求△ABC的面积.解答:解:(1)因为向量
 .
.∴f(x)=
 sinxcosx+cos2x=
sinxcosx+cos2x= +
+ =sin(2x+
=sin(2x+ )+
)+ ,
,∴f(x)的单调增区间为:[
 ],k∈Z.
],k∈Z.函数的单调减区间为
 ,k∈Z.
,k∈Z.(2)由
 ,所以
,所以 ,
,∴sin(A+
 )=
)= ,
,∵A是三角形内角,∴A+
 ∈(
∈( ),∴A=
),∴A= 或A=
或A= ,
,又
 ,∴A=
,∴A= ,
,由正弦定理可得sinB=
 =
= ,⇒B=
,⇒B= 或
或 ,
,C=π-A-B=
 或
或
所以△ABC的面积为:
 =
= =
= ,
,或
 =
= =
= .
.点评:本题考查向量的数量积两角和的正弦函数的应用,正弦定理,正弦函数的单调性,三角形的面积的求法,考查计算能力,转化思想的应用,分类讨论思想的应用.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
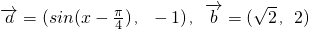 且
且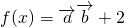
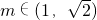 ,求x1+x2的值.
,求x1+x2的值.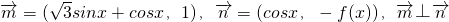 .
.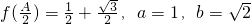 ,求△ABC的面积.
,求△ABC的面积.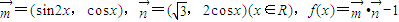 ,
,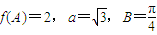 ,求b的值.
,求b的值.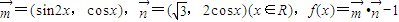 ,
,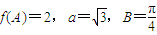 ,求b的值.
,求b的值. ,
,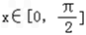 上的值域;
上的值域;