题目内容
已知向量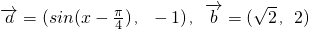 且
且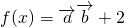
(1)求f(x)的表达式.
(2)用“五点作图法”画出函数f(x)在一个周期上的图象.
(3)写出f(x)在[-π,π]上的单调递减区间.
(4)设关于x的方程f(x)=m在x∈[-π,π]上的根为x1,x2且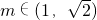 ,求x1+x2的值.
,求x1+x2的值.
解:(1)由向量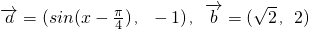 ,
,
所以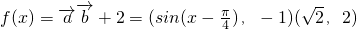 +2
+2
=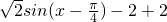 =
= .
.
(2)函数f(x)的周期为2π.
列表:

描点并用平滑曲线连接:
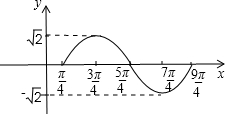
(3)由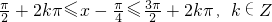
得 .
.
当K=-1时,得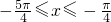 ;当k=0时,得
;当k=0时,得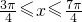 .
.
所以f(x)在[-π,π]上的单调递减区间为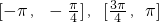 .
.
(4)由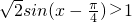 ,得
,得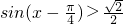 .
.
因为x∈[-π,π],所以 .
.
所以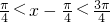 ,则
,则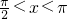 .
.
所以当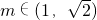 时方程f(x)=m的两个根x1,x2关于x=
时方程f(x)=m的两个根x1,x2关于x= 对称.
对称.
所以x1+x2= .
.
分析:(1)直接把向量的坐标代入解析式,利用数量积的坐标运算化简;
(2)由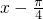 分别取0,
分别取0, ,π,
,π, ,2π求出x的值进行列表,然后描点用平滑曲线连接;
,2π求出x的值进行列表,然后描点用平滑曲线连接;
(3)利用复合函数的单调性求出函数f(x)的单调区间,通过取k得值求出f(x)在[-π,π]上的单调递减区间;
(4)分析得到满足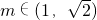 时关于x的方程f(x)=m在x∈[-π,π]上的根x1,x2在
时关于x的方程f(x)=m在x∈[-π,π]上的根x1,x2在 内切关于x=
内切关于x= 对称,利用中点坐标公式求x1+x2的值.
对称,利用中点坐标公式求x1+x2的值.
点评:本题考查了平面向量的数量积运算,训练了利用五点作图法作函数的图象,训练了复合函数单调性的求法,考查了函数零点的判断方法,该题考查知识点多,训练了学生综合处理问题的能力,是中档题.
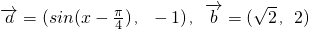 ,
,所以
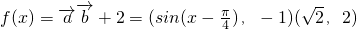 +2
+2=
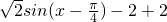 =
= .
.(2)函数f(x)的周期为2π.
列表:

描点并用平滑曲线连接:

(3)由
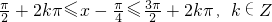
得
 .
.当K=-1时,得
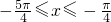 ;当k=0时,得
;当k=0时,得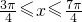 .
.所以f(x)在[-π,π]上的单调递减区间为
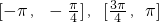 .
.(4)由
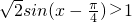 ,得
,得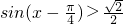 .
.因为x∈[-π,π],所以
 .
.所以
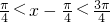 ,则
,则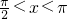 .
.所以当
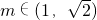 时方程f(x)=m的两个根x1,x2关于x=
时方程f(x)=m的两个根x1,x2关于x= 对称.
对称.所以x1+x2=
 .
.分析:(1)直接把向量的坐标代入解析式,利用数量积的坐标运算化简;
(2)由
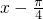 分别取0,
分别取0, ,π,
,π, ,2π求出x的值进行列表,然后描点用平滑曲线连接;
,2π求出x的值进行列表,然后描点用平滑曲线连接;(3)利用复合函数的单调性求出函数f(x)的单调区间,通过取k得值求出f(x)在[-π,π]上的单调递减区间;
(4)分析得到满足
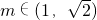 时关于x的方程f(x)=m在x∈[-π,π]上的根x1,x2在
时关于x的方程f(x)=m在x∈[-π,π]上的根x1,x2在 内切关于x=
内切关于x= 对称,利用中点坐标公式求x1+x2的值.
对称,利用中点坐标公式求x1+x2的值.点评:本题考查了平面向量的数量积运算,训练了利用五点作图法作函数的图象,训练了复合函数单调性的求法,考查了函数零点的判断方法,该题考查知识点多,训练了学生综合处理问题的能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
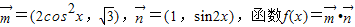 .
.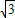 ,且a>b,求a,b的值.
,且a>b,求a,b的值.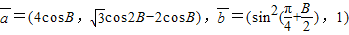 ,
,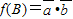
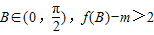 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.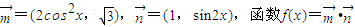 .
.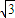 ,且a>b,求a,b的值.
,且a>b,求a,b的值.
 。
。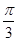 +x)的值;
+x)的值;