题目内容
(1)当m>n>3(m,n∈Z)时,证明:(nmm)n>(mnn)m.
(2)已知函数f(x)=alnx-(x-1)2-ax(常数a>0),如果对于f(x)的图象上两点P1(x1,f(x1)),P2(x2,f(x2))(x1<x2),存在x0∈(x1,x2),使得f(x)的图象在x=x0处的切线m∥P1P2,求证:x0<
.
(2)已知函数f(x)=alnx-(x-1)2-ax(常数a>0),如果对于f(x)的图象上两点P1(x1,f(x1)),P2(x2,f(x2))(x1<x2),存在x0∈(x1,x2),使得f(x)的图象在x=x0处的切线m∥P1P2,求证:x0<
| x1+x2 | 2 |
分析:(1)将不等式两边取自然对数,变形可得原不等式等价于nlnn+mnlnm>mlnm+mnlnn.注意到n-m是正数,采用放缩:先证明nlnn+mnlnm>mlnm+mnlnn+(n-m),等价变形为
>
.因此考察函数F(x)=
,利用导数研究F(x)的单调性得到F(x)在(3,+∞)上是增函数,从而得到F(m)>F(n),即
>
成立,即可得到当m>n>3(m,n∈Z)时,不等式(nmm)n>(mnn)m成立.
(2)由f(x)的图象在x=x0处的切线m∥P1P2,列出等式化简得f'(x0)=
-(x1+x2-2)-a.求出f'(x)的表达式得f'(
)=
-(x1+x2-2)-a.根据f'(x)在区间(0,+∞)上是减函数,得到不等式x0<
等价于f'(x0)>f'(
),化简得到ln
>
.令g(t)=lnt-
,其中t=
>1,证出g(t)在(1,+∞)上是增函数,得到g(t)>0,因此lnt>
,可得
>
,再将t还原为
即可证出f'(x0)>f'(
),从而得到x0<
,原不等式成立.
| m(1+lnm) |
| m-1 |
| n(1+lnn) |
| n-1 |
| x(1+lnx) |
| x-1 |
| m(1+lnm) |
| m-1 |
| n(1+lnn) |
| n-1 |
(2)由f(x)的图象在x=x0处的切线m∥P1P2,列出等式化简得f'(x0)=
aln
| ||
| x2-x1 |
| x1+x2 |
| 2 |
| 2a |
| x1+x2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x2 |
| x1 |
| 2(x2-x1) |
| x1+x2 |
| 2(t-1) |
| t+1 |
| x2 |
| x1 |
| 2(t-1) |
| t+1 |
| lnt |
| t-1 |
| 2 |
| t+1 |
| x2 |
| x1 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
解答:解:(1)不等式(nmm)n>(mnn)m,等价于ln[(nmm)n]>ln[(mnn)m]
即nln(nmm)>mln(mnn),等价于nlnn+mnlnm>mlnm+mnlnn,…(*)
考虑到n>m得n-m>0,为了证明上式成立,先证明nlnn+mnlnm>mlnm+mnlnn+(n-m),
整理得0<n(m-1)(1+lnn)<m(n-1)(1+lnm),等价于
>
,
考察函数F(x)=
,得F'(x)=
=
,
∵t=x-2-lnx的导数t'=1-
>0在(3,+∞)上成立,
∴F'(x)≥F'(4)>0,可得F(x)=
在(3,+∞)上是增函数,
从而得到F(m)>F(n),可得
>
成立,因此得到(*)式成立.
综上所述,可得当m>n>3(m,n∈Z)时,不等式(nmm)n>(mnn)m成立.
(2)根据题意,得f'(x0)= kP1P2=
=
-(x1+x2-2)-a,
∵f'(x)=
-2(x-1)-a,
∴f'(
)=
-(x1+x2-2)-a,且f'(x)在区间(0,+∞)上是减函数
要证x0<
,只需证明f'(x0)>f'(
),
即证
>
,即ln
>
.
令t=
>1,g(t)=lnt-
,得g'(t)=
-
=
>0
∴g(t)在(1,+∞)上是增函数,可得g(t)>g(1)=0,
由此可得lnt>
,即
>
,将t还原为
得ln
>
.
因此,f'(x0)>f'(
),可得x0<
,原不等式成立.
即nln(nmm)>mln(mnn),等价于nlnn+mnlnm>mlnm+mnlnn,…(*)
考虑到n>m得n-m>0,为了证明上式成立,先证明nlnn+mnlnm>mlnm+mnlnn+(n-m),
整理得0<n(m-1)(1+lnn)<m(n-1)(1+lnm),等价于
| m(1+lnm) |
| m-1 |
| n(1+lnn) |
| n-1 |
考察函数F(x)=
| x(1+lnx) |
| x-1 |
| (2+lnx)(x-1)-x(1+lnx) |
| (x-1)2 |
| x-2-lnx |
| (x-1)2 |
∵t=x-2-lnx的导数t'=1-
| 1 |
| x |
∴F'(x)≥F'(4)>0,可得F(x)=
| x(1+lnx) |
| x-1 |
从而得到F(m)>F(n),可得
| m(1+lnm) |
| m-1 |
| n(1+lnn) |
| n-1 |
综上所述,可得当m>n>3(m,n∈Z)时,不等式(nmm)n>(mnn)m成立.
(2)根据题意,得f'(x0)= kP1P2=
| f(x1)-f(x2) |
| x1-x2 |
aln
| ||
| x2-x1 |
∵f'(x)=
| a |
| x |
∴f'(
| x1+x2 |
| 2 |
| 2a |
| x1+x2 |
要证x0<
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
即证
aln
| ||
| x2-x1 |
| 2a |
| x1+x2 |
| x2 |
| x1 |
| 2(x2-x1) |
| x1+x2 |
令t=
| x2 |
| x1 |
| 2(t-1) |
| t+1 |
| 1 |
| t |
| 4 |
| (t+1)2 |
| (t-1)2 |
| t(t+1)2 |
∴g(t)在(1,+∞)上是增函数,可得g(t)>g(1)=0,
由此可得lnt>
| 2(t-1) |
| t+1 |
| lnt |
| t-1 |
| 2 |
| t+1 |
| x2 |
| x1 |
| x2 |
| x1 |
| 2(x2-x1) |
| x1+x2 |
因此,f'(x0)>f'(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
点评:本题着重考查了利用导数研究函数的单调性与最值、不等式的等价变形、用分析法证明不等式和导数的几何意义等知识,考查转化化归和数形结合的数学思想、逻辑推理能力、计算能力和分析问题解决问题的综合能力,属于中档题.

练习册系列答案
相关题目
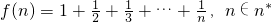 ,求证:
,求证: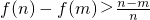 ;
;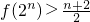 ;
;