题目内容
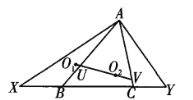
【题目】如图,在![]() 中,X、Y为直线BC上两点(X、B、C、Y顺次排列),使得
中,X、Y为直线BC上两点(X、B、C、Y顺次排列),使得![]() .设
.设![]() 的外心分别为
的外心分别为![]() ,直线
,直线![]() 与AB、AC分别交于点U、V.证明:
与AB、AC分别交于点U、V.证明:![]() 为等腰三角形.
为等腰三角形.
【答案】见解析
【解析】
证法1 如图所示,作![]() 的平分线,与BC交于点P.设
的平分线,与BC交于点P.设![]() 的外接圆分别为
的外接圆分别为![]() .
.
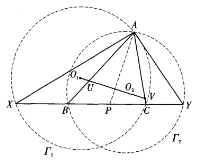
由内角平分线的性质知![]() .
.
由条件得![]() .
.
故![]()
![]() .
.
则点P对![]() 的幂相等.从而,点P在圆
的幂相等.从而,点P在圆![]() 的根轴上.
的根轴上.
于是,![]() .这表明,点U、V关于直线AP对称.
.这表明,点U、V关于直线AP对称.
因此,![]() 为等腰三角形.
为等腰三角形.
证法2 如图所示,设![]() 的外心为O,联结
的外心为O,联结![]() .过点
.过点![]() 分别作直线BC的垂线,垂足分别为
分别作直线BC的垂线,垂足分别为![]() .
.![]() 作于点K.
作于点K.
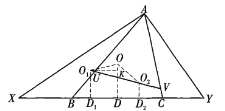
下面证明:![]() .
.
在![]() 中,
中,
![]() .
.
由外心的性质,知![]() .
.
又![]() ,故
,故![]() .
.
而![]() 分别为BC、CX的中点,则
分别为BC、CX的中点,则
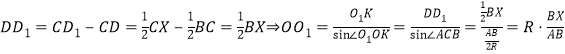 ,
,
其中,R为![]() 的外接圆半径.
的外接圆半径.
类似地,![]() .
.
由已知条件得
![]() .
.
由![]() .
.
类似地,![]() .
.
又因为![]() ,所以,
,所以,
![]() ,
,
![]() .
.
因此,![]() 为等腰三角形.
为等腰三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某科研单位在研发钛合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值![]() (
(![]() 值越大产品的性能越好)与这种新合金材料的含量
值越大产品的性能越好)与这种新合金材料的含量![]() (单位:克)的关系:当
(单位:克)的关系:当![]() 时,
时,![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时,![]() .测得部分数据如表所示.
.测得部分数据如表所示.
| 0 | 2 | 6 | 10 | … |
| -4 | 8 | 8 |
| … |
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求该新合金材料的含量![]() 为何值时产品的性能达到最佳.
为何值时产品的性能达到最佳.