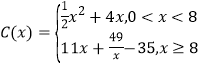题目内容
【题目】某科研单位在研发钛合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值![]() (
(![]() 值越大产品的性能越好)与这种新合金材料的含量
值越大产品的性能越好)与这种新合金材料的含量![]() (单位:克)的关系:当
(单位:克)的关系:当![]() 时,
时,![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时,![]() .测得部分数据如表所示.
.测得部分数据如表所示.
| 0 | 2 | 6 | 10 | … |
| -4 | 8 | 8 |
| … |
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求该新合金材料的含量![]() 为何值时产品的性能达到最佳.
为何值时产品的性能达到最佳.
【答案】(1)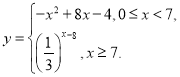 ;(2)4.
;(2)4.
【解析】
(1)当![]() 时,设出二次函数解析式,代入点
时,设出二次函数解析式,代入点![]() 坐标列方程组,解方程组求得函数解析式.当
坐标列方程组,解方程组求得函数解析式.当![]() 时,将
时,将![]() 代入
代入![]() ,由此求得
,由此求得![]() 的值.从而求得
的值.从而求得![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)利用二次函数的性质求得当![]() 时
时![]() 的最大值,根据指数函数的单调性求得当
的最大值,根据指数函数的单调性求得当![]() 时函数
时函数![]() 的最大值,由此确定出当
的最大值,由此确定出当![]() 时,产品的性能达到最佳.
时,产品的性能达到最佳.
(1)当![]() 时,
时,![]() 是
是![]() 的二次函数,可设
的二次函数,可设![]()
![]() .依题意有
.依题意有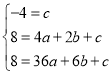 ,解得:
,解得:![]() ,
,![]() ,
,![]() ,即
,即![]()
![]() .
.
当![]() 时,
时,![]() ,由
,由![]() ,
,![]() 可得
可得![]() ,即
,即![]()
![]() .
.
综上可得
(2)当![]() 时,
时,![]() ,即当
,即当![]() 时,
时,![]() 取得最大值12;
取得最大值12;
当![]() 时,
时,![]() 单调递减,可得
单调递减,可得![]() ,即当
,即当![]() 时,
时,![]() 取得最大值3.
取得最大值3.
综上可得,该新合金材料的含量![]() 为4时产品的性能达到最佳.
为4时产品的性能达到最佳.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目