题目内容
已知数列 的前
的前 项和为
项和为 ,且
,且 是
是 和
和 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 的取值范围.
的取值范围.
【答案】
(1)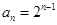 ,
,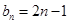 ;(2)
;(2)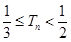
【解析】
试题分析:(1)由已知得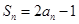 ,再利用
,再利用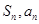 的关系,将其转化为关于
的关系,将其转化为关于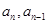 的递推式,得
的递推式,得 ,故数列
,故数列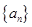 是公比为2的等比数列,进而求其通项公式,等差数列
是公比为2的等比数列,进而求其通项公式,等差数列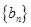 中,由于知道两项,先求首项和公差,进而求通项公式;(2)求数列前n项和,先考虑其通项公式,根据通项公式的特点,选择相应的求和方法,该题
中,由于知道两项,先求首项和公差,进而求通项公式;(2)求数列前n项和,先考虑其通项公式,根据通项公式的特点,选择相应的求和方法,该题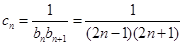 ,故可采取裂项相消法,求得
,故可采取裂项相消法,求得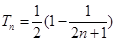 ,看作自变量为
,看作自变量为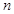 的函数,进而求值域得
的函数,进而求值域得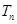 的取值范围.
的取值范围.
试题解析:(1)∵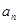 是
是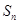 和
和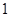 的等差中项,∴
的等差中项,∴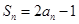 ,当
,当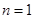 时,
时, ,∴
,∴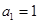
当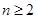 时,
时,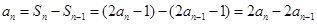 , ∴
, ∴ ,即
,即

∴数列 是以
是以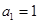 为首项,
为首项,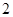 为公比的等比数列,∴
为公比的等比数列,∴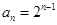 ,
,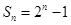 ,设
,设 的公差为
的公差为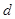 ,
,
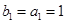 ,
, ,∴
,∴ ,∴
,∴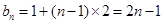 .
.
(2)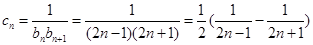 ,∴
,∴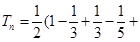
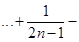

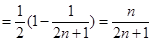 ,∵
,∵ 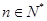 ,∴
,∴ ,
,
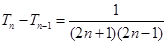
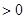 ,∴数列
,∴数列 是一个递增数列 ∴
是一个递增数列 ∴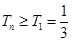 .
.
综上所述,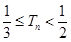
考点:1、等差数列的通项公式和等差中项;2、等比数列的通项公式;3、数列求和.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,满足
,满足 .
. 为等比数列,并
为等比数列,并 求出
求出 ;
; ,求
,求 的最大项.
的最大项. }的前
}的前 项和为
项和为 ,且
,且 (
( );
); =3
=3 (
(


 ;
; }的通项公式
}的通项公式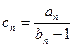 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且
,且 .
.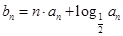 ,数列
,数列 的前
的前 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.