题目内容
已知方程(m+2)x+(m-3)y+4=0(m∈R)所表示的直线恒过定点,试求该定点的坐标.
思路解析:可以从两个角度考虑:
(1)因为直线恒过定点,故该定点坐标与m的取值无关,于是我们可令m取一些特定值,进而求出两不同直线的公共点.
(2)将方程变形为m(x+y)+2x-3y+4=0.依题意,定点的坐标与m的取值无关,于是m的系数x+y必为0,进而2x-3y+4=0.
解法一:令m=-2,则方程变为-5y+4=0,故y=![]() .
.
令m=3,则方程变为5x+4=0,
故x=![]() .
.
依题意可知,直线恒过定点(![]() ,
,![]() ).
).
解法二:将方程变形为m(x+y)+2x-3y+4=0.
依题意,定点的坐标与m的取值无关,于是此定点的坐标必然满足x+y=0且2x-3y+4=0.
解方程组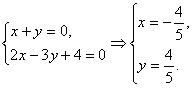
∴定点的坐标为(![]() ,
,![]() ).
).
绿色通道:求含参数的直线方程恒过定点时,可赋予参数两个具体的值,通过解方程组求交点;也可整理成f1(x,y)+λf2(x,y)=0的形式,再求交点.

练习册系列答案
相关题目