题目内容
(本小题满分12分)椭圆C: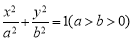 的长轴是短轴的两倍,点
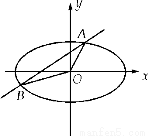
的长轴是短轴的两倍,点 在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为
在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为 、
、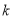 、
、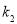 ,且
,且 、
、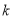 、
、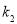 恰好构成等比数列,记△
恰好构成等比数列,记△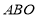 的面积为S.
的面积为S.
(Ⅰ)求椭圆C的方程.
(Ⅱ)试判断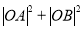 是否为定值?若是,求出这个值;若不是,请说明理由?
是否为定值?若是,求出这个值;若不是,请说明理由?
(Ⅲ)求S的范围.
(1)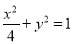 ,(2)5,(3)
,(2)5,(3)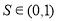
【解析】
试题分析:首先借助椭圆的标准方程借助待定系数法求出 得出椭圆方程,第二步设直线
得出椭圆方程,第二步设直线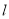 的方程
的方程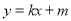
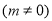 ,设而不求联立方程组,消去
,设而不求联立方程组,消去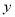 得出关于
得出关于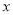 的一元二次方程,根据根与系数关系,得出
的一元二次方程,根据根与系数关系,得出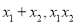 ,根据直线OA、l、OB的斜率分别为
,根据直线OA、l、OB的斜率分别为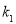 、
、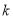 、
、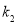 ,且
,且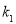 、
、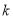 、
、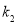 恰好构成等比数列,有
恰好构成等比数列,有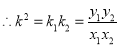 ,借助
,借助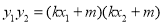 ,找出
,找出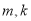 关系,进而求出
关系,进而求出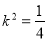 ,代入
,代入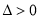 ,得出
,得出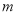 的范围,最后表示
的范围,最后表示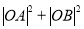 ,把
,把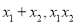 代入后得出定值;第三步先求弦长
代入后得出定值;第三步先求弦长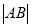 ,再求原点到直线
,再求原点到直线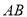 的距离,表示出三角形的面积,再利用
的距离,表示出三角形的面积,再利用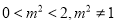 ,得出面积的取值范围.
,得出面积的取值范围.
试题解析:(1)由题意可知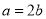 且
且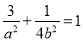
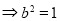 ,
,
所以椭圆的方程为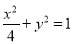
(2)设直线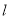 的方程为
的方程为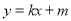
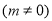 ,
, 由
由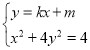
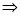
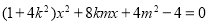
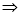

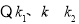 恰好构成等比数列.
恰好构成等比数列.
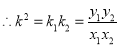 =
=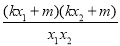 即
即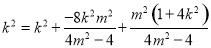
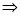
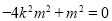
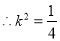
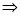
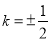 ,此时且
,此时且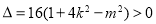
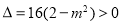 ,得
,得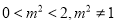 ,
,
(否则: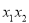
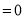 ,则
,则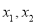 中至少有一个为
中至少有一个为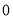 ,直线
,直线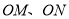 中至少有一个斜率不存在,矛盾!);
中至少有一个斜率不存在,矛盾!);
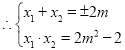 ,
,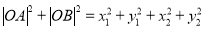 =
=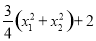
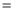
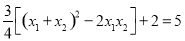
所以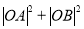 是定值为
是定值为 .
.
(3)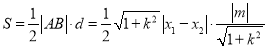
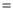
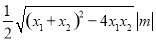 =
=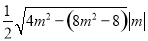
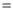
 (
(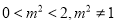 ),则:
),则: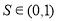
考点:1.求椭圆方程;2.设而不求解题思想;3.减元思想;4.定点定值问题的解题方法;5.取值范围问题;

练习册系列答案
相关题目
 中,
中, ,
, ,
, ,那么数列
,那么数列 的前
的前 项和等于
项和等于  B.
B. C.
C. D.
D.
 ”的 ( )
”的 ( ) 有公共焦点,且离心率
有公共焦点,且离心率 的双曲线方程为( )
的双曲线方程为( ) B.
B. C.
C. D.
D.
 ,且
,且 ,则
,则 的最小值为___________.
的最小值为___________. 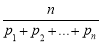 为
为 个正数
个正数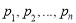 的“均倒数”.若已知正数数列
的“均倒数”.若已知正数数列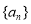 的前
的前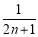 ,又
,又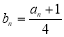 ,则
,则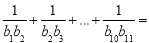 ( )
( )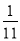 B.
B.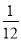 C.
C.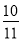 D.
D.
 时,不等式
时,不等式 恒成立,则
恒成立,则 的取值范围是 .
的取值范围是 . 满足
满足 ,则
,则 的最大值___________;
的最大值___________;