题目内容
函数y=ex-e的图象与两坐标轴围成的封闭区域面积为
1
1
.分析:解方程ex-e=0得x=1,故所求的阴影部分面积=
(-ex+e)dx.计算出答案即可.
| ∫ | 1 0 |
解答:解:令ex-e=0,解得x=1,因此其函数图象为:
故所求的阴影部分面积=
(-ex+e)dx=(-ex+ex)
=1.
故答案为1.

故所求的阴影部分面积=
| ∫ | 1 0 |
| | | 1 0 |
故答案为1.
点评:把已知求面积问题转化为利用定积分求面积是解题的关键.

练习册系列答案
相关题目
函数y=
的图象大致为( )
| ex+e-x |
| ex-e-x |
A、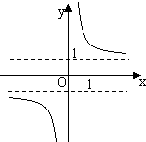 |
B、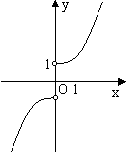 |
C、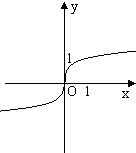 |
D、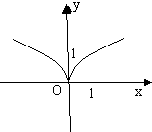 |
