题目内容
设斜率为1的直线l过抛物线y2=ax（a＞0）的焦点F，且和y轴交于点A，若△OAF（O为坐标原点）的面积为8，则a的值为 ．
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：由题意得，在直角△OAF中，|AO|=|OF|，且|OF|=|
|，代入三角形的面积公式，求解即可．
| a |
| 4 |
解答：
解：∵斜率为1的直线l过抛物线y2=ax的焦点F，且与y轴相交于点A，
∴|AO|=|OF|，且|OF|=|
|，∴△OAF的面积为
×|
|×|
|=8，
解得a=16或-16，
故答案为：±16．
∴|AO|=|OF|，且|OF|=|
| a |
| 4 |
| 1 |
| 2 |
| a |
| 4 |
| a |
| 4 |
解得a=16或-16，
故答案为：±16．
点评：本题考查抛物线的方程与几何性质、直线与抛物线的位置关系等基础知识，注意仔细的斜率是解题的关键之一．属基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知A、B分别为椭圆x2+
=1的左右顶点，P是椭圆上第一象限的任一点，若∠PAB=α，∠PBA=β，则必有（ ）
| y2 |
| 2 |
| A、2tanα+cotβ=0 |
| B、2tanα-cotβ=0 |
| C、tanα+2cotβ=0 |
| D、tanα-2cosβ=0 |
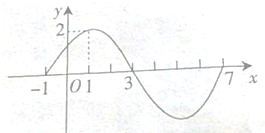如图为函数y1=Asin（ωx+φ）的一段图象，已知A＞0，ω＞0，φ∈（-