题目内容
已知向量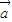 =(cosx,sinx),
=(cosx,sinx),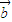 =(-cosx,cosx),函数f(x)=2
=(-cosx,cosx),函数f(x)=2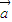 •
•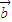 +1.
+1.(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x∈[0,2π]时,求f(x)的单调减区间.
【答案】分析:(1)先根据向量的数量积运算表示出函数f(x)的解析式,然后再由三角函数二倍角公式和辅角公式化简为y=Asin(wx+ρ)+b的形式,根据T= 得到答案.
得到答案.
(2)将2x- 看作一个整体,使其满足
看作一个整体,使其满足 求出x的范围,再由x∈[0,2π]求交集即可.
求出x的范围,再由x∈[0,2π]求交集即可.
解答:解:(Ⅰ)因为f(x)=2 •
• +1=2(cosx,sinx)•(-cosx,cosx)+1=2(-cos2x+sinxcosx)+1
+1=2(cosx,sinx)•(-cosx,cosx)+1=2(-cos2x+sinxcosx)+1
=1-2cos2x+2sinxcosx=sin2x-cos2x
=
所以f(x)的最小正周期是
(Ⅱ)依条件得
解得
又
即当x∈[0,2π]时,f(x)的单调减区间是
点评:本题主要考查向量的数量积运算和三角函数的基本性质.三角函数和向量的综合题是高考的热点,每年必考,要给予重视.
 得到答案.
得到答案.(2)将2x-
 看作一个整体,使其满足
看作一个整体,使其满足 求出x的范围,再由x∈[0,2π]求交集即可.
求出x的范围,再由x∈[0,2π]求交集即可.解答:解:(Ⅰ)因为f(x)=2
 •
• +1=2(cosx,sinx)•(-cosx,cosx)+1=2(-cos2x+sinxcosx)+1
+1=2(cosx,sinx)•(-cosx,cosx)+1=2(-cos2x+sinxcosx)+1=1-2cos2x+2sinxcosx=sin2x-cos2x
=

所以f(x)的最小正周期是

(Ⅱ)依条件得

解得

又

即当x∈[0,2π]时,f(x)的单调减区间是

点评:本题主要考查向量的数量积运算和三角函数的基本性质.三角函数和向量的综合题是高考的热点,每年必考,要给予重视.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目