题目内容
已知数列![]() 满足
满足![]() ,且
,且![]() .
.
⑴ 求证:当![]() 时,
时,![]() ;
;
⑵ 若![]() 对任意的
对任意的![]() (
(![]() )恒成立, 求
)恒成立, 求![]() 的最大值.
的最大值.
证明:(Ⅰ)①当![]() 时,
时,![]() ,又
,又![]() ,
, ![]() ,
,
∴![]() .
.
②假设![]() 时,
时, ![]() 成立,
成立,
当![]() 时,有
时,有![]() ,
,
∴![]() 成立,
成立,
由假设![]() 有
有![]() ,
,
∴![]() , ∴
, ∴![]() .
.
故由①, ②知,对任意![]() 都有
都有![]() 成立.
成立.
(Ⅱ)由于![]()
![]()
![]() ,
,
![]() ,
,
①当![]() 时,显然不可能使
时,显然不可能使![]() 对任意
对任意![]() 成立,
成立,
②当![]() 时,
时, ![]() 对任意
对任意![]() 有可能成立,
有可能成立,
当![]() 时,
时,![]() ,
,
假设![]() ,由
,由![]() ,
,![]()
所以![]() 时,对任意
时,对任意![]() 都有
都有![]() 成立,
成立,
所以![]() 时,
时,![]() ,
,
故![]() 的最大值是
的最大值是![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 满足
满足 ,且
,且 (
( )
) ,
, ,
, (2)由(1)猜想
(2)由(1)猜想 ;
; 满足
满足 ,且
,且 (
( )。
)。 、
、 、
、 的值;
的值; 满足
满足 ,且
,且 (n
(n 2且n∈N*).
2且n∈N*). 的通项公式;(5分)
的通项公式;(5分) ,求
,求 ,并证明:
,并证明: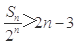 .(7分)
.(7分) 满足
满足 ,且
,且 ,且
,且 ,则数列
,则数列
 B.
B. C.
C. D.
D.