题目内容
已知数列![]() 满足:
满足:![]() 且
且
![]() .
.
(Ⅰ)求![]() ,
,![]() ,
,![]() ,
,![]() 的值及数列
的值及数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅰ)经计算![]() ,
,![]() ,
,![]() ,
,![]() .
.
数列![]() 的通项公式为
的通项公式为
(Ⅱ)![]() .
.
解析:
(Ⅰ)经计算![]() ,
,![]() ,
,![]() ,
,![]() . …………….2分
. …………….2分
当![]() 为奇数时,
为奇数时,![]() ,即数列
,即数列![]() 的奇数项成等差数列,
的奇数项成等差数列,
![]() ; …………………………….4分
; …………………………….4分
当![]() 为偶数,
为偶数,![]() ,即数列
,即数列![]() 的偶数项成等比数列,
的偶数项成等比数列,
![]() .…………………………….6分
.…………………………….6分
因此,数列![]() 的通项公式为
的通项公式为 . ………………………7分
. ………………………7分
(Ⅱ)![]()
![]() ,
,
![]() ……(1)
……(1)
![]() …(2)
…(2)
(1)、(2)两式相减,
得![]()

![]() .
.
![]() .……………………………….14分
.……………………………….14分

练习册系列答案
相关题目
 满足
满足 ,且
,且 (
( )
) ,
, ,
, (2)由(1)猜想
(2)由(1)猜想 ;
; 满足
满足 ,且
,且 (
( )。
)。 、
、 、
、 的值;
的值; 满足
满足 ,且
,且 (n
(n 2且n∈N*).
2且n∈N*). 的通项公式;(5分)
的通项公式;(5分) ,求
,求 ,并证明:
,并证明: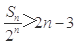 .(7分)
.(7分) 满足
满足 ,且
,且 ,且
,且 ,则数列
,则数列
 B.
B. C.
C. D.
D.