题目内容
16.在椭圆$\frac{x^2}{4}$+y2=1中,F1,F2为椭圆的左右焦点,P是直线x=4上的一个动点.则∠F1PF2取得最大值时线段OP的长为$\frac{π}{3}$.分析 在椭圆$\frac{x^2}{4}$+y2=1中,如图所示,设P(4,t),不妨设t≥0,t=0时,∠F1PF2=0.t>0时,${k}_{P{F}_{1}}$=$\frac{t}{4+\sqrt{3}}$,${k}_{P{F}_{2}}$=$\frac{t}{4-\sqrt{3}}$.∠F1PF2为锐角.tan∠F1PF2=$\frac{|{k}_{P{F}_{1}}-{k}_{P{F}_{2}}|}{1+{k}_{P{F}_{1}}{k}_{P{F}_{2}}|}$,代入利用基本不等式的性质即可得出.
解答 解:在椭圆$\frac{x^2}{4}$+y2=1中,c=$\sqrt{4-1}$=$\sqrt{3}$.
∴F1$(-\sqrt{3},0)$,F2$(\sqrt{3},0)$.
如图所示,设P(4,t),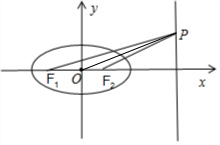
不妨设t≥0,t=0时,∠F1PF2=0.
t>0时,${k}_{P{F}_{1}}$=$\frac{t}{4+\sqrt{3}}$,${k}_{P{F}_{2}}$=$\frac{t}{4-\sqrt{3}}$.
∵∠F1PF2为锐角.
tan∠F1PF2=$\frac{|{k}_{P{F}_{1}}-{k}_{P{F}_{2}}|}{1+{k}_{P{F}_{1}}{k}_{P{F}_{2}}|}$=$\frac{\frac{t}{4-\sqrt{3}}-\frac{t}{4+\sqrt{3}}}{1+\frac{t}{4-\sqrt{3}}×\frac{t}{4+\sqrt{3}}}$=$\frac{2\sqrt{3}t}{1+{t}^{2}}$=$\frac{2\sqrt{3}}{t+\frac{1}{t}}$≤$\frac{2\sqrt{3}}{2\sqrt{t•\frac{1}{t}}}$=$\sqrt{3}$,
当且仅当t=1时取等号,tan∠F1PF2取到最大值,
此时∠F1PF2最大,故∠F1PF2的最大值为$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查了椭圆的标准方程及其性质、直线夹角公式、斜率计算公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 若|$\overrightarrow{a}$|确定,则θ唯一确定 | B. | 若|$\overrightarrow{b}$|确定,则θ唯一确定 | ||
| C. | 若θ确定,则|$\overrightarrow{b}$|唯一确定 | D. | 若θ确定,则|$\overrightarrow{a}$|唯一确定 |
| A. | 10 | B. | -$\frac{9}{2}$ | C. | 20 | D. | -20 |
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 3 | D. | $\sqrt{3}$ |
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |