题目内容
9．如图，已知正三棱锥V-ABC，底面积为16$\sqrt{3}$，一条侧棱长为2$\sqrt{6}$，计算它的高和斜高．
分析 取AB中点D，连结CD，作VO⊥底面ABC，垂足为O，由已知求出AB=8，OC=$\frac{8\sqrt{3}}{3}$，DO=$\frac{4\sqrt{3}}{3}$，由此利用勾股定理能求出它的高和斜高．
解答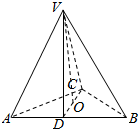 
解：取AB中点D，连结CD，作VO⊥底面ABC，垂足为O，
∵正三棱锥V-ABC，底面积为16$\sqrt{3}$，一条侧棱长为2$\sqrt{6}$，
∴O∈CD，$\frac{1}{2}×AB×AB×sin60°$=$16\sqrt{3}$，解得AB=8，
∴OC=$\frac{2}{3}CD=\frac{2}{3}\sqrt{64-16}$=$\frac{2}{3}×4\sqrt{3}$=$\frac{8\sqrt{3}}{3}$，
∵侧棱长VO=2$\sqrt{6}$，∴高VO=$\sqrt{（2\sqrt{6}）^{2}-（\frac{8\sqrt{3}}{3}）^{2}}$=$\frac{2\sqrt{6}}{3}$．
∵DO=$\frac{1}{3}CD$=$\frac{1}{3}\sqrt{64-16}$=$\frac{4\sqrt{3}}{3}$，
∴斜率VD=$\sqrt{V{O}^{2}+D{O}^{2}}$=$\sqrt{（2\sqrt{6}）^{2}+（\frac{4\sqrt{3}}{3}）^{2}}$=$\frac{2\sqrt{66}}{3}$．
点评 本题考查正三棱锥的高和斜高的求法，是中档题，解题时要认真审题，注意勾股定理的合理运用．
练习册系列答案
相关题目
20．设函数f（n）=k（k∈N+），k是π的小数点后的第n位数字，π=3.1415926535…，则$\underset{\underbrace{f（f…f（f（10）））}}{n个f}$（n≥6）等于（ ）
| A． | 1 | B． | 0 | C． | -1 | D． | 2 |
4．将函数$y=\sqrt{3}cosx+sinx，（x∈R）$的图象向右平移θ（θ＞0）个单位长度后，所得到的图象关于y轴对称，则θ的最小值是（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{6}$ |
14．已知三棱锥的底面是边长为a的正三角形，则过各侧棱中点的截面的面积为（ ）
| A． | $\frac{\sqrt{3}}{4}{a}^{2}$ | B． | $\frac{\sqrt{4}}{8}{a}^{2}$ | C． | $\frac{\sqrt{3}}{16}{a}^{2}$ | D． | $\frac{\sqrt{13}}{32}{a}^{2}$ |
如图，四棱锥P-ABCD的底面是边长为2的菱形，∠BAD=60°，△PAD是等边三角形，且$PB=\sqrt{6}$，M是棱PC上除P、C的任意一点，且$\frac{PM}{PC}=λ$