题目内容
平行六面体ABCDA1B1C1D1中，向量
、
、
两两的夹角均为60°，且|
|=1，|
|=2，|
|=3，则|
|等于（ ）
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AA1 |
| AC1 |
分析：由题设知
=
+
+
，故
2=（
+
+
）2，由此能求出|
|．
| AC1 |
| AB |
| BC |
| CC1 |
| AC1 |
| AB |
| BC |
| CC1 |
| AC1 |
解答：解：如图，∵平行六面体ABCD-A1B1C1D1中，
向量
、
、
两两的夹角均为60°，
且|
|=1，|
|=2，|
|=3，
∴
=
+
+
，
∴
2=（
+
+
）2
=
2+
2+
2+2
•
+2
•
+2
•
=1+4+9+2×1×2×cos60°+2×1×3×cos60°+2×2×3×cos60°
=25，
∴|
|=5．
故选A．
向量
| AB |
| AD |
| AA1 |
且|
| AB |
| AD |
| AA1 |
∴
| AC1 |
| AB |
| BC |
| CC1 |
∴
| AC1 |
| AB |
| BC |
| CC1 |
=
| AB |
| BC |
| CC1 |
| AB |
| BC |
| AB |
| CC1 |
| BC |
| CC1 |
=1+4+9+2×1×2×cos60°+2×1×3×cos60°+2×2×3×cos60°
=25，
∴|
| AC1 |
故选A．
点评：本题以平行六面体为载体考查向量在几何中的应用，解题时要认真审题，关键是利用条件向量
、
、
两两的夹角均为60°，进行合理转化．
| AB |
| AD |
| AA1 |
练习册系列答案
同步练习强化拓展系列答案
相关题目
如图，在平行六面体ABCD-A1B1C1D1中，已知| AB |
| AD |
| AA1 |
| a |
| b |
| c |
| BD1 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
如图，已知平行六面体OABC-O1A1B1C1，点G是上底面O1A1B1C1的中心，且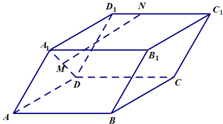
如图：在平行六面体ABCD-A1B1C1D1中，点M是线段A1D的中点，点N在线段C1D1上，且
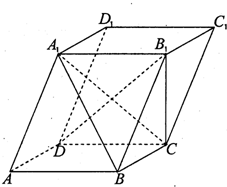（2011•重庆三模）如题19图，平行六面体ABCD-A1B1C1D1的下底面ABCD是边长为a的正方形，AA1=