题目内容

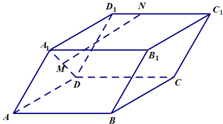如图：在平行六面体ABCD-A1B1C1D1中，点M是线段A1D的中点，点N在线段C1D1上，且D1N=
1
3
D1C1，∠A1AD=∠A1AB=60°，∠BAD=90°，AB=AD=AA1=1．
（1）求满足
MN
=x
AB
+y
AD
+z
AA1
的实数x、y、z的值．
（2）求AC1的长．
分析：（1）首先
MN
=
MD1
+
D1N
，    又可知
MD1
=
AM=
1
2
(
AA1
+
AD
)， 且
D1N=
1
3
D1C1
=
1
3
AB
，代入化简整理即可．
（2）利用向量的方法，
AC1
=
AD
+
AB
+
AA1
，求其平方后再开方即可．
解答：解：（1）
MN
=
MD1
+
D1N
=
1
2
(
AA1
+
AD
)+
1
3
AB
=
1
3
AB
+
1
2
AD
+
1
2
AA1

所以x=
1
3
，y=
1
2
，z=
1
2
…（4分）
（2）∵
AC1
=
AD
+
AB
+
AA1

∴|AC1|2=(
AD
+
AB
+
AA1
)2
=
AD
2+
AB
2+
AA1
2+2
AD
•
AB
+2
AD
•
AA1
+2
AB
•
AA1
=1+1+1+0+1+1
=5

∴AC1=
5
…..（8分）
点评：本题考查了空间向量基本定理，向量的应用：求线段长度．考查转化、计算能力．
练习册系列答案
相关题目
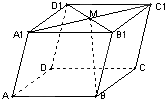精英家教网如图：在平行六面体ABCD-A1B1C1D1中，M为A1C1与B1D1的交点．若
AB
=
a
，
AD
=
b
，
AA1
=
c
，则下列向量中与
BM
相等的向量是（　　）
A、-
1
2
a
+
1
2
b
+
c
B、
1
2
a
+
1
2
b
+
c
C、-
1
2
a
-
1
2
b
+
c
D、
1
2
a-
1
2
b+c
精英家教网如图，在平行六面体ABCD-A1B1C1D1中，已知
AB
=a，
AD
=b，
AA1
=c，则用向量
a
，
b
，
c
可表示向量
BD1
=（　　）
A、
a
+
b
+
c
B、
a
-
b
+
c
C、
a
+
b
-
c
D、-
a
+
b
-
c
精英家教网对于向量a，b，定义a×b为向量a，b的向量积，其运算结果为一个向量，且规定a×b的模|a×b|=|a||b|sinθ（其中θ为向量a与b的夹角），a×b的方向与向量a，b的方向都垂直，且使得a，b，a×b依次构成右手系．如图，在平行六面体ABCD-EFGH中，∠EAB=∠EAD=∠BAD=60°，AB=AD=AE=2，则(
AB
×
AD
)•
AE
=（　　）
A、4
B、8
C、2
2
D、4
2
精英家教网如图，在平行六面体ABCD-A1B1C1D1中，若
AB
=
a
，
AD
=
b
，
AA1
=
c
，则
D1B
=（　　）
A、
a
+
b
-
c
B、
a
+
b
+
c
C、
a
-
b
-
c
D、-
a
+
b
+
c
（2001•上海）如图，在平行六面体ABCD-A1B1C1D1中，M为AC与BD的交点，若
A1B1
=
a
，
A1D1
=
b
，
A1A
=
c
．则下列向量中与
B1M
相等的向量是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网