题目内容
设函数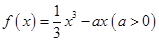 ,
,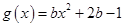 .
.
(1)若曲线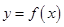 与
与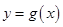 在它们的交点
在它们的交点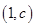 处有相同的切线,求实数
处有相同的切线,求实数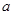 、
、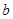 的值;
的值;
(2)当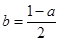 时,若函数
时,若函数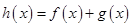 在区间
在区间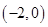 内恰有两个零点,求实数
内恰有两个零点,求实数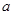 的取值范围;
的取值范围;
(3)当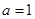 ,
,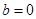 时,求函数
时,求函数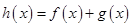 在区间
在区间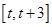 上的最小值.
上的最小值.
【答案】
(1) ;(2)
;(2)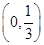 ;(3)
;(3)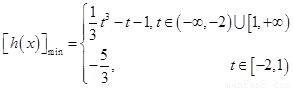 .
.
【解析】
试题分析:(1)从条件“曲线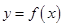 与
与 在它们的交点
在它们的交点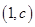 处有相同的切线”得到
处有相同的切线”得到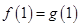 以及
以及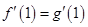 ,从而列有关
,从而列有关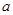 、
、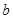 的二元方程组,从而求出
的二元方程组,从而求出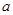 与
与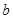 的值;(2)将
的值;(2)将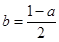 代入函数
代入函数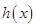 的解析式,利用导数分析函数
的解析式,利用导数分析函数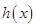 在区间
在区间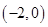 上的单调性,确定函数
上的单调性,确定函数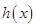 在区间
在区间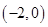 上是单峰函数后,然后对函数
上是单峰函数后,然后对函数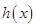 的端点值与峰值进行限制,列不等式组解出
的端点值与峰值进行限制,列不等式组解出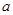 的取值范围;(3)将
的取值范围;(3)将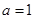 ,
,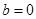 代入函数
代入函数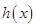 的解析式,并求出函数
的解析式,并求出函数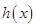 的单调区间,对函数
的单调区间,对函数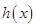 的极值点是否在区间
的极值点是否在区间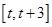 内进行分类讨论,结合函数的单调性确定函数
内进行分类讨论,结合函数的单调性确定函数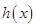 在区间
在区间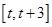 上的最小值.
上的最小值.
试题解析:(1)因为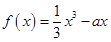 ,
,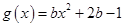 ,所以
,所以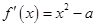 ,
,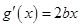 .
.
因为曲线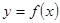 与
与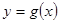 在它们的交点
在它们的交点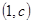 处有相同切线,
处有相同切线,
所以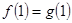 ,且
,且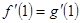 ,
,
即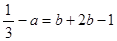 ,且
,且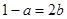 ,解得
,解得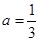 ,
,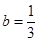 ;
;
(2)当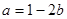 时,
时,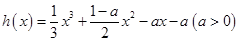 ,
,
所以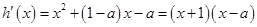 ,
,
令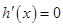 ,解得
,解得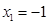 ,
,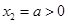 ,
,
当 变化时,
变化时,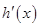 、
、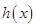 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以函数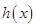 的单调递增区间为
的单调递增区间为 、
、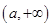 ,单调递减区间为
,单调递减区间为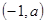 .
.
故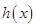 在区间
在区间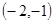 内单调递增,在区间
内单调递增,在区间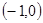 内单调递减.
内单调递减.
从而函数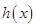 在区间
在区间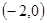 内恰有两个零点,当且仅当
内恰有两个零点,当且仅当 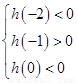 ,
,
即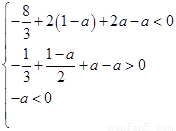 ,解得
,解得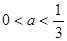 .
.
所以实数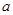 的取值范围是
的取值范围是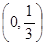 .
.
(3)当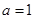 ,
,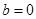 时,
时,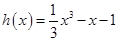 .
.
所以函数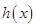 的单调递增区间为
的单调递增区间为 、
、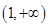 ,单调递减区间为
,单调递减区间为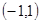 .
.
由于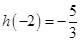 ,
,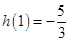 ,所以
,所以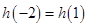 .
.
①当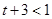 ,即
,即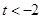 时,
时,
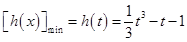 ;
;
②当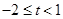 时,
时,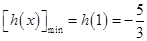 ;
;
③当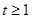 时,
时,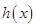 在区间
在区间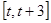 上单调递增,
上单调递增,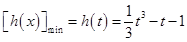 ;
;
综上可知,函数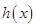 在区间
在区间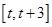 上的最小值为
上的最小值为
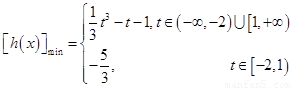 .
.
考点:1.导数的几何意义;2.函数的零点;3.函数的最值;4.分类讨论

练习册系列答案
相关题目
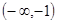
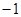
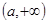

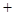
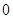

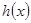
 ,集合
,集合 .
. ,求
,求 解析式。
解析式。 ,且
,且 时的最小值为
时的最小值为 ,求实数
,求实数 的值。
的值。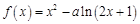 (
(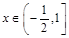 ,
, ).
).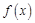 在其定义域内是减函数,求
在其定义域内是减函数,求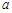 的取值范围;
的取值范围;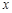 的值,并证明你的结论.
的值,并证明你的结论.