题目内容
【题目】设![]() 是偶函数,且当
是偶函数,且当![]() 时,
时,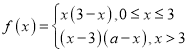
(1)当![]() 时,求
时,求![]() 的解析式;
的解析式;
(2)设函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,试求
,试求![]() 的表达式;
的表达式;
(3)若方程![]() 有四个不同的实根,且它们成等差数列,试探求
有四个不同的实根,且它们成等差数列,试探求![]() 与
与![]() 满足的条件.
满足的条件.
【答案】(1)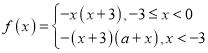 ;(2)
;(2)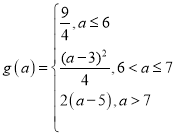 ;(3)
;(3)![]() 与
与![]() 满足的条件为
满足的条件为![]() 且
且![]() ,或
,或![]() 且
且![]() ,或
,或![]() 且
且![]() .
.
【解析】
(1)设![]() 、
、![]() ,利用已知函数的解析式,即可求得结论;
,利用已知函数的解析式,即可求得结论;
(2)因为![]() 是偶函数,所以它在区间
是偶函数,所以它在区间![]() ,
,![]() 上的最大值即为它在区间
上的最大值即为它在区间![]() ,
,![]() 上的最大值,分类讨论,即可求得结论;
上的最大值,分类讨论,即可求得结论;
(3)设这四个根从小到大依次为![]() ,
,![]() ,
,![]() ,
,![]() ,则当方程
,则当方程![]() 在
在![]() ,
,![]() 上有四个实根时,由
上有四个实根时,由![]() ,且
,且![]() ,得
,得![]() ,
,![]() ,从而
,从而![]() ,且要求
,且要求![]() 对
对![]() 恒成立,由此可得结论.
恒成立,由此可得结论.
解:(1)当![]() 时,
时,![]()
同理,当![]() 时,
时,![]() ,
,
所以,当![]() 时,
时,![]() 的解析式为
的解析式为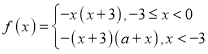
(2)因为![]() 是偶函数,所以它在区间
是偶函数,所以它在区间![]() 上的最大值即为它在区间
上的最大值即为它在区间![]() 上的最大值,
上的最大值,
①当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,所以
上单调递减,所以![]()
②当![]() 时,
时,![]() 在
在![]() 与
与![]() 上单调递增,在
上单调递增,在![]() 与
与![]() 上单调递减,
上单调递减,
所以此时只需比较![]() 与
与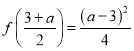 的大小.
的大小.
(i)当![]() 时,
时,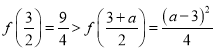 ,所以
,所以![]()
(ii)当![]() 时,
时, ,
,
所以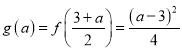
③当![]() 时,
时,![]() 在
在![]() 与
与![]() 上单调递增,在
上单调递增,在![]() 上单调递减,且
上单调递减,且![]() ,
,
所以![]() .
.
综上所述,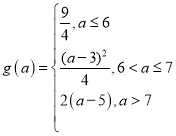 .
.
(3)设这四个根从小到大依次为![]() ,
,![]() ,
,![]() ,
,![]() .
.
①当方程![]() 在
在![]() 上有四个实根时,由
上有四个实根时,由![]() ,且
,且![]() ,得
,得![]() ,
,![]() ,
,
从而![]() ,且要求
,且要求![]() 对
对![]() 恒成立.
恒成立.
(i)当![]() 时,
时,![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 对
对![]() 恒成立,
恒成立,
即![]() 适合题意.
适合题意.
(ii)当![]() 时,欲
时,欲![]() 对
对![]() 恒成立,只要
恒成立,只要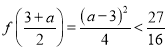 ,
,
解得![]() ,故此时应满足
,故此时应满足![]() .
.
②当方程![]() 在
在![]() 上有两个实根时,
上有两个实根时,![]() ,且
,且![]() ,
,![]() ,
,
所以必须满足![]() ,且
,且![]() ,
,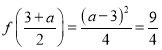 ,解得
,解得![]() .
.
③当方程![]() 在
在![]() 上无实根时,
上无实根时,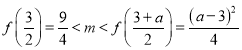 ,
,![]() ,
,
由![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,
,
所以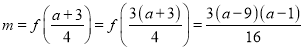 ,
,
且由![]() ,解得
,解得![]() .
.
综上所述,![]() 与
与![]() 满足的条件为
满足的条件为![]() 且
且![]() ,或
,或![]() 且
且![]() ,
,
或![]() 且
且![]() .
.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为n的样本,得到一周参加社区服务时间的统计数据如下:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(1)求m,n;
(2)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(3)从该校学生中随机调查60名学生,一周参加社区服务时间超过1小时的人数记为X,以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,求X的分布列和数学期望.
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2![]() .
.