题目内容
 从椭圆
从椭圆| x2 |
| a2 |
| y2 |
| b2 |
| MN |
| OP |
(1)求该椭圆的离心率;
(2)若过右焦点F2且不与坐标轴垂直的直线l交椭圆C于A、B两点,点A关于x轴的对称点为A1,直线A1B与x轴交于点R(4,0),求椭圆C的方程.
分析:(1)令x=-c,得y=
,所以点P的坐标为(-c,
),由
=λ
,(λ>0)得到离心率.
(2)设直线l的方程为:x=my+c,(m≠0),与椭圆方程
+
=1,联立得到(m2+2)y2+2mcy-c2=0y2+2mcy-c2=0.记A(x1,y1),B(x2,y2),再由韦达定理结合题设条件能够求出所求椭圆方程.
| b2 |
| a |
| b2 |
| a |
| MN |
| OP |
(2)设直线l的方程为:x=my+c,(m≠0),与椭圆方程
| x2 |
| 2c2 |
| y2 |
| c2 |
解答:解:(1)令x=-c,得y=
,所以点P的坐标为(-c,
),(2分)
由
=λ
,(λ>0)得到:
=
,(4分)
所以b=c,a2=2c2,即离心率e=
(6分)
(2)设直线l的方程为:x=my+c,(m≠0),与椭圆方程
+
=1,
联立得到:(m2+2)y2+2mcy-c2=0y2+2mcy-c2=0.(8分)
记A(x1,y1),B(x2,y2),
则y1+y2=
,y1y2=
,(9分)
由A关于x轴的对称点为A1,得A1(x1,-y1),
则直线A1B的方程是:
=
,过点R(4,0)得到:
y1(my2-my1)=4(y2+y1)-(my1+c)(y2+y1)(10分)
即:2my1y2=(4-c)(y1+y2)
所以:
=(4-c)•
,
得到:c=4-c,所以:c=2(12分)
所以所求椭圆方程为:
+
=1.(13分)
| b2 |
| a |
| b2 |
| a |
由
| MN |
| OP |
| ||
| c |
| b |
| a |
所以b=c,a2=2c2,即离心率e=
| ||
| 2 |
(2)设直线l的方程为:x=my+c,(m≠0),与椭圆方程
| x2 |
| 2c2 |
| y2 |
| c2 |
联立得到:(m2+2)y2+2mcy-c2=0y2+2mcy-c2=0.(8分)
记A(x1,y1),B(x2,y2),
则y1+y2=
| -2mc |
| m2+2 |
| -c2 |
| m2+2 |
由A关于x轴的对称点为A1,得A1(x1,-y1),
则直线A1B的方程是:
| y+y1 |
| y2+y1 |
| x-x1 |
| x2-x1 |
y1(my2-my1)=4(y2+y1)-(my1+c)(y2+y1)(10分)
即:2my1y2=(4-c)(y1+y2)
所以:
| -2mc 2 |
| m2+2 |
| -2mc |
| m2+2 |
得到:c=4-c,所以:c=2(12分)
所以所求椭圆方程为:
| x2 |
| 8 |
| y2 |
| 4 |
点评:本题考查椭圆的离心率和椭圆方程的求法,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,注意椭圆性质的灵活运用.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
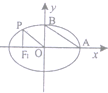 如图,从椭圆
如图,从椭圆 (2009年)从椭圆
(2009年)从椭圆