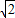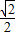题目内容
 (2009年)从椭圆
(2009年)从椭圆| x2 |
| a2 |
| y2 |
| b2 |
分析:先计算PF1的长,再利用两直线平行得tan∠POF1,最后在直角三角形POF1中,找到a、b、c间的等式,从而求出离心率
解答:解:设F1(-c,0),将x=-c代入
+
=1(a>b>0),得y=±
∴PF1=
,OF1=c
∵AB∥OP,∴tan∠POF1=tan∠BAO=
∴在直角三角形POF1中,tan∠POF1=
=
=
∴b=c,∴a=
c
∴e=
=
故选D
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
∴PF1=
| b2 |
| a |
∵AB∥OP,∴tan∠POF1=tan∠BAO=
| b |
| a |
∴在直角三角形POF1中,tan∠POF1=
| PF1 |
| OF1 |
| b2 |
| ac |
| b |
| a |
∴b=c,∴a=
| 2 |
∴e=
| c |
| a |
| ||
| 2 |
故选D
点评:本题考查了椭圆的几何性质,椭圆离心率的求法,将已知几何条件转化为椭圆特征量a、b、c间的关系,是解决本题的关键

练习册系列答案
相关题目
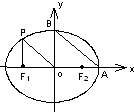 (2009年)从椭圆
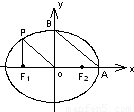
(2009年)从椭圆 上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP(O为坐标原点),则该椭圆的离心率为
上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP(O为坐标原点),则该椭圆的离心率为



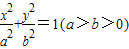 上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP(O为坐标原点),则该椭圆的离心率为( )
上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP(O为坐标原点),则该椭圆的离心率为( )