题目内容
如图,在多面体ABCD中,DB⊥平面ABC,AE∥BD,且AB=BC=CA=BD=2AE=2
(I)求证:平面ECD⊥平面BCD
(II)求二面角D-EC-B的正切值
(III)求三棱锥A-ECD的体积
(I)求证:平面ECD⊥平面BCD
(II)求二面角D-EC-B的正切值
(III)求三棱锥A-ECD的体积

证明:(I)分别取CD,CB的中点F,G,连结EF、FG,AG,易证AG⊥面CBD,AG∥EF, ∴平面ECD⊥平面BCD
∴平面ECD⊥平面BCD

(II)解:连结BF,则BF⊥CD,由(I)知,BF⊥面ECD,过F作FM⊥EC,垂足为M,连结MB,则∠BMF为二面角D—EC—B的平面角,由题意知, ,
,
 ,
,
(III)
 ∴平面ECD⊥平面BCD
∴平面ECD⊥平面BCD
(II)解:连结BF,则BF⊥CD,由(I)知,BF⊥面ECD,过F作FM⊥EC,垂足为M,连结MB,则∠BMF为二面角D—EC—B的平面角,由题意知,
 ,
, ,
,
(III)

略

练习册系列答案
相关题目
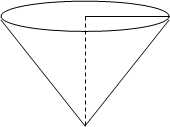
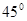 ,容器的高为
,容器的高为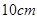 .制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到
.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到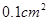 )
)
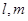 ,平面
,平面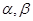 满足
满足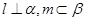 ,则
,则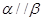 是
是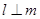 的( )
的( )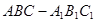 中,
中, 是
是 的中点,
的中点,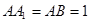
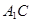 ∥平面
∥平面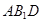 ;
;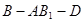 的大小.
的大小.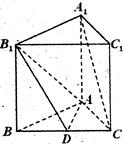
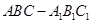 中的每一个顶点都在同一个球面上,如果
中的每一个顶点都在同一个球面上,如果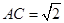 ,
,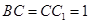 ,
,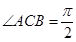 ,那么
,那么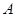 、
、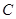 两点间的球面距离是
两点间的球面距离是  若CM=BN=a(0<a<
若CM=BN=a(0<a<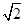 ).
).
 且法向量为
且法向量为 的平面的方程是
的平面的方程是 ”。现知道平面
”。现知道平面 的方程为
的方程为 ,则过
,则过 与
与 的直线与平面
的直线与平面 弦值是
弦值是