题目内容
已知函数 .
.
(1)设函数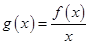 ,当
,当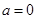 时,讨论
时,讨论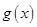 的单调性;
的单调性;
(2)若函数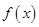 在
在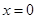 处取得极小值,求
处取得极小值,求 的取值范围.
的取值范围.
(1)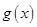 在
在 上单减,在
上单减,在 上单增;(2)
上单增;(2) .
.
解析试题分析:(1)首先求导数,当 时,函数单调递减;当
时,函数单调递减;当 时,单调递增;(2)
时,单调递增;(2) ,显然
,显然 ,要使得函数
,要使得函数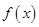 在
在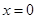 处取得极小值,需使
处取得极小值,需使 在
在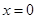 左侧为负,右侧为正.令
左侧为负,右侧为正.令 ,则只需
,则只需 在
在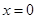 左、右两侧均为正即可.结合图象可知,只需
左、右两侧均为正即可.结合图象可知,只需 即可,从而可得
即可,从而可得 的取值范围.
的取值范围.
试题解析:(1)
 , 2分
, 2分
显然当 时,
时, ,
, ,当
,当 时,
时, ,
, 在
在 上单减,在
上单减,在 上单增; 6分
上单增; 6分
(2) ,
,
显然 ,要使得函数
,要使得函数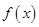 在
在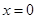 处取得极小值,需使
处取得极小值,需使 在
在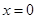 左侧为负,右侧为正.令
左侧为负,右侧为正.令 ,则只需
,则只需 在
在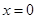 左、右两侧均为正即可
左、右两侧均为正即可
亦即只需 ,即
,即
 . .12分
. .12分
(原解答有误, 与
与 轴不可能有两个不同的交点)
轴不可能有两个不同的交点)
考点:导数的应用.

练习册系列答案
相关题目
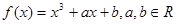 的图象记为E.过点
的图象记为E.过点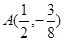 作曲线E的切线,这样的切线有且仅有两条,求
作曲线E的切线,这样的切线有且仅有两条,求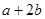 的值.
的值.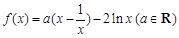 .
.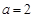 ,求曲线
,求曲线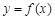 在点
在点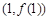 处的切线方程;
处的切线方程;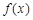 的单调区间;
的单调区间;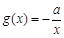 .若至少存在一个
.若至少存在一个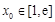 ,使得
,使得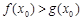 成立,求实数
成立,求实数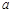 的取值范围.
的取值范围.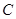 :
: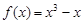
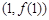 处的切线方程;
处的切线方程;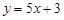 平行的曲线C的切线方程.
平行的曲线C的切线方程.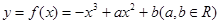
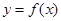 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;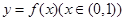 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求 的充要条件;
的充要条件; .
.
 R).
R).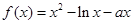 ,
, .
.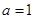 时,求
时,求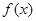 的最小值;
的最小值;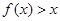 ,求a的取值范围.
,求a的取值范围.