题目内容
已知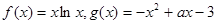 .
.
(1)求函数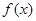 在
在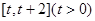 上的最小值;
上的最小值;
(2)对一切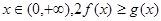 恒成立,求实数
恒成立,求实数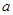 的取值范围;
的取值范围;
(3)证明:对一切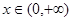 ,都有
,都有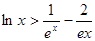 成立.
成立.
【答案】
(1)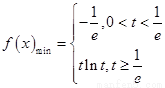 ;(2)
;(2) ;
;
(3)设 ,则
,则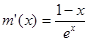 ,
,
证得 ,当且仅当
,当且仅当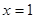 时取到,
时取到,
从而对一切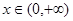 ,都有
,都有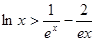 成立.
成立.
【解析】
试题分析:(1)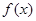 定义域为
定义域为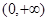 ,
,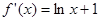 ,
,
当 单调递减,
单调递减,
当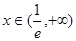 ,
,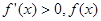 单调递增.
2分
单调递增.
2分
①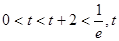 无解; 3分
无解; 3分
②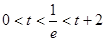 ,即
,即 时,
时,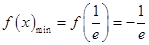
③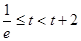 ,即
,即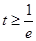 时,
时,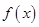 在
在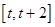 上单调递增,
上单调递增,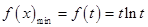
所以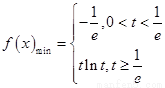
(2)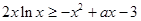 ,则
,则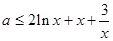 ,对一切
,对一切 恒成立
恒成立
设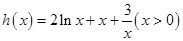 ,则
,则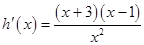
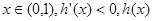 单调递减,
单调递减,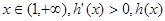 单调递增
8分
单调递增
8分
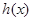 在
在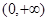 上,有唯一极小值
上,有唯一极小值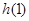 ,即为最小值.
,即为最小值.
所以 ,因为对一切
,因为对一切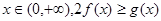 恒成成立,
恒成成立,
所以 ;
9分
;
9分
(3)问题等价于证明 ,
,
由(1)可知 的最小值是
的最小值是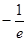 ,当且仅当
,当且仅当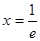 时取到,
时取到,
设 ,则
,则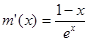 ,
,
易得 ,当且仅当
,当且仅当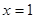 时取到, 11分
时取到, 11分
从而对一切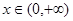 ,都有
,都有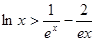 成立.
12分
成立.
12分
考点:本题主要考查应用导数研究函数的单调性及极值,不等式的证明。
点评:典型题,本题属于导数应用中的基本问题,(2)(3)涉及恒成立问题、不等式证明问题,均通过转化成求函数的最值,这种思路是一般解法,在研究函数最值的过程中,再次利用导数。

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
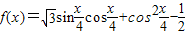 .
.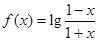 .
.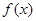 的定义域;
的定义域;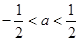 ,试比较
,试比较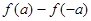 与
与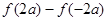 的大小.
的大小.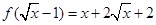 ,
,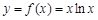 .
.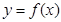 的图像在
的图像在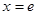 处的切线方程;
处的切线方程;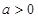 ,求函数
,求函数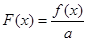 在
在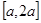 上的最大值;
上的最大值;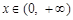 ,都有
,都有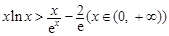 成立。
成立。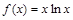 .
. 在区间
在区间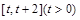 上的最小值;
上的最小值;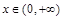 ,
, 恒成立,求实数
恒成立,求实数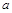 的取值范围;
的取值范围;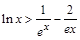 恒成立.
恒成立.