题目内容
函数f(x)、f(x+2)均为偶函数,且当x∈[0,2]时,f(x)是减函数,设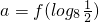 ,b=f(7.5),c=f(-5),则a、b、c的大小关系是
,b=f(7.5),c=f(-5),则a、b、c的大小关系是
- A.b>a>c
- B.a>c>b
- C.a>b>c
- D.c>a>b
C
分析:由条件“函数f(x)、f(x+2)均为偶函数”可知f(x)的周期为T=4,根据周期性和偶函数将 ,7.5,-5化到区间[0,2]上,而当x∈[0,2]时,f(x)是减函数,大小关系很快见分晓.
,7.5,-5化到区间[0,2]上,而当x∈[0,2]时,f(x)是减函数,大小关系很快见分晓.
解答:由题意“函数f(x)、f(x+2)均为偶函数”可知,
f(x+2)=f(-x+2)=f(-(2-x))=f(x-2)
?f(x+2)=f(x-2)
?f((x-2)+4)=f(x-2)
?f(t+4)=f(t)
∴f(x)的周期为t=4.
从而 ,
,
b=f(7.5)=f(8-0.5)=f(-0.5)=f(0.5),
c=f(-5)=f(5)=f(4+1)=f(1),
∵ .
.
故选C.
点评:本题主要考查了函数奇偶性的应用,以及函数的周期性和比较大小,属于基础题.
分析:由条件“函数f(x)、f(x+2)均为偶函数”可知f(x)的周期为T=4,根据周期性和偶函数将
 ,7.5,-5化到区间[0,2]上,而当x∈[0,2]时,f(x)是减函数,大小关系很快见分晓.
,7.5,-5化到区间[0,2]上,而当x∈[0,2]时,f(x)是减函数,大小关系很快见分晓.解答:由题意“函数f(x)、f(x+2)均为偶函数”可知,
f(x+2)=f(-x+2)=f(-(2-x))=f(x-2)
?f(x+2)=f(x-2)
?f((x-2)+4)=f(x-2)
?f(t+4)=f(t)
∴f(x)的周期为t=4.
从而
 ,
,b=f(7.5)=f(8-0.5)=f(-0.5)=f(0.5),
c=f(-5)=f(5)=f(4+1)=f(1),
∵
 .
.故选C.
点评:本题主要考查了函数奇偶性的应用,以及函数的周期性和比较大小,属于基础题.

练习册系列答案
相关题目
 ;
; 的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.
的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.