题目内容
经过M(2,1)作直线L交双曲线x2-
=1于A、B两点,且M为AB的中点,
(1)求直线L的方程;
(2)求线段AB的长.
| y2 | 2 |
(1)求直线L的方程;
(2)求线段AB的长.
分析:(1)设A(x1,y1),B(x2,y2),则x1+x2=4,y1+y2=2,由x12-
=1,x22-
=1,得(x1+x2)(x1-x2)-
(y1+y2)(y1-y2)=0,所以kAB=
=4,由此能求出直线L的方程.
(2)把y=4x-7代入x2-
=1消去y得14x2-56x+51=0,所以x1+x2=4,x1•x2=
,由此能求出求线段AB的长.
| y12 |
| 2 |
| y22 |
| 2 |
| 1 |
| 2 |
| y1-y2 |
| x1-x2 |
(2)把y=4x-7代入x2-
| y2 |
| 2 |
| 51 |
| 14 |
解答:解:(1)设A(x1,y1),B(x2,y2),
∵M(2,1)为AB的中点,
∴x1+x2=4,y1+y2=2,
把A(x1,y1),B(x2,y2)分别代入双曲线x2-
=1,
得x12-
=1,x22-
=1,
二者相减,得(x1+x2)(x1-x2)-
(y1+y2)(y1-y2)=0,
把x1+x2=4,y1+y2=2代入,得4(x1-x2)-(y1-y2)=0,
所以kAB=
=4
∴直线L的方程为y=4x-7
(2)把y=4x-7代入x2-
=1,
消去y得14x2-56x+51=0,
∴x1+x2=4,x1•x2=
,k=4,
∴|AB|=
=
=
.
从而得|AB|=
.
∵M(2,1)为AB的中点,
∴x1+x2=4,y1+y2=2,
把A(x1,y1),B(x2,y2)分别代入双曲线x2-
| y2 |
| 2 |
得x12-
| y12 |
| 2 |
| y22 |
| 2 |
二者相减,得(x1+x2)(x1-x2)-
| 1 |
| 2 |
把x1+x2=4,y1+y2=2代入,得4(x1-x2)-(y1-y2)=0,
所以kAB=
| y1-y2 |
| x1-x2 |
∴直线L的方程为y=4x-7
(2)把y=4x-7代入x2-
| y2 |
| 2 |
消去y得14x2-56x+51=0,
∴x1+x2=4,x1•x2=
| 51 |
| 14 |
∴|AB|=
| (1+k2)[(x1+x2)2-4x1x2] |
=
17(16-4×
|
| ||
| 7 |
从而得|AB|=
| ||
| 7 |
点评:本题考查直线和双曲线的位置关系的综合运用,考查中点弦方程的求法和弦长公式的应用.解题时要认真审题,注意点差法的灵活运用.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
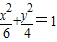 于S、T两点,且M是ST的中点,求直线l的方程.
于S、T两点,且M是ST的中点,求直线l的方程.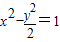 于A、B两点,且M为AB的中点,
于A、B两点,且M为AB的中点,