题目内容
7.若在区间[0,e]内随机取一个数x,则代表数x的点到区间两端点距离均大于$\frac{e}{3}$的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
分析 根据几何概型计算公式,用区间[$\frac{1}{3}$e,$\frac{2}{3}$e]的长度除以区间[0,e]的长度,即可得到本题的概率.
解答 解:解:∵区间[0,e]的长度为e-0=e,x的点到区间两端点距离均大于$\frac{e}{3}$,长度为$\frac{e}{3}$,
∴在区间[0,e]内随机取一个数x,则代表数x的点到区间两端点距离均大于$\frac{e}{3}$的概率为P=$\frac{1}{3}$
故选:C
点评 本题主要考查了几何概型,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.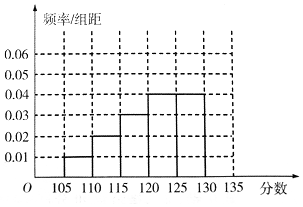 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
(Ⅰ)补全所给的频率分布直方图,并求n,x,y的值;
(Ⅱ)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取9份进行展出,并从9份试卷中选出两份作为优秀试卷,优秀试卷在[115,120)中的分数记为ξ,求随机变量ξ的分布列及期望.
 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:| 组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
| 第一组 | [105,110] | 15 | 0.3 |
| 第二组 | [110,115) | 30 | 0.3 |
| 第三组 | [115,120) | x | 0.4 |
| 第四组 | [120,125) | 100 | 0.5 |
| 第五组 | [125,130) | 120 | 0.6 |
| 第六组 | [130,135) | 195 | y |
(Ⅱ)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取9份进行展出,并从9份试卷中选出两份作为优秀试卷,优秀试卷在[115,120)中的分数记为ξ,求随机变量ξ的分布列及期望.
15.已知抛物线y2=4x,过焦点F作直线与抛物线交于点A,B(点A在x轴下方),点A1与点A关于x轴对称,若直线AB斜率为1,则直线A1B的斜率为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
17.圆C与x轴相切于T(1,0),与y轴正半轴交于两点A、B,且|AB|=2,则圆C的标准方程为( )
| A. | (x-1)2+(y-$\sqrt{2}$)2=2 | B. | (x-1)2+(y-2)2=2 | C. | (x+1)2+(y+$\sqrt{2}$)2=4 | D. | (x-1)2+(y-$\sqrt{2}$)2=4 |
 为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.
为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.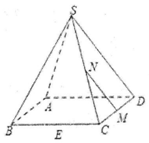 如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论:
如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论: