题目内容
设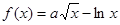
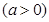
(1)若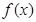 在
在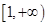 上递增,求
上递增,求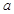 的取值范围;
的取值范围;
(2)求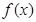 在
在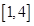 上的最小值.
上的最小值.
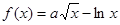
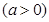
(1)若
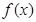 在
在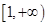 上递增,求
上递增,求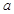 的取值范围;
的取值范围;(2)求
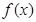 在
在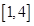 上的最小值.
上的最小值.(1) (2)
(2)
 (2)
(2)
(I)由题意知 在
在 上恒成立,从而转化为在
上恒成立,从而转化为在 时
时  恒成立问题来解决.
恒成立问题来解决.
(2)先求出
 ,然后再分
,然后再分 或
或 或
或 三种情况讨论f(x)的最小值.
三种情况讨论f(x)的最小值.
解:(1)
在 时
时  恒成立
恒成立
 在
在 时
时 

 .
.
(2)由

(a)当 时,在
时,在 上
上 ∴
∴ ;
;
(b)当 时,在
时,在 上
上 ∴
∴ ;
;
(c)当 时,在
时,在 上
上 ,在
,在 上
上 ,
,
此时 .
.
综上所述:
 在
在 上恒成立,从而转化为在
上恒成立,从而转化为在 时
时  恒成立问题来解决.
恒成立问题来解决.(2)先求出

 ,然后再分
,然后再分 或
或 或
或 三种情况讨论f(x)的最小值.
三种情况讨论f(x)的最小值.解:(1)

在
 时
时  恒成立
恒成立 在
在 时
时 

 .
.(2)由


(a)当
 时,在
时,在 上
上 ∴
∴ ;
;(b)当
 时,在
时,在 上
上 ∴
∴ ;
;(c)当
 时,在
时,在 上
上 ,在
,在 上
上 ,
,此时
 .
.综上所述:


练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
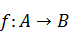 ,其中集合
,其中集合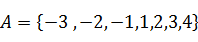 ,集合
,集合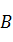 中的元素都是
中的元素都是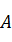 中元素在映射
中元素在映射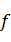 下的象,且对于任意的
下的象,且对于任意的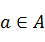 ,在
,在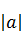 ,则集合
,则集合 ,且
,且 则
则
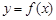 是偶函数,
是偶函数,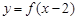 在[0,2]上是单调减函数,则( )
在[0,2]上是单调减函数,则( )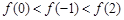
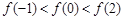
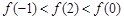
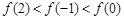
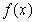 ,对任意的
,对任意的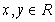 ,有
,有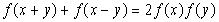 ,且
,且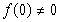 .
.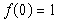 ; (2)求证:
; (2)求证: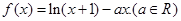
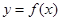 的单调区间;
的单调区间;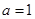 时,求
时,求 在定义域上的最大值;
在定义域上的最大值;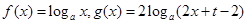
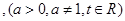 .
.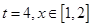 ,且
,且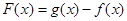 有最小值2时,求
有最小值2时,求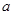 的值;
的值;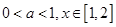 时,有
时,有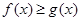 恒成立,求实数
恒成立,求实数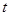 的取值范围.
的取值范围. ,则
,则

