题目内容
(本小题满分12分)已知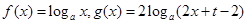
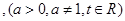 .
.
(1)当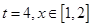 ,且
,且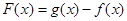 有最小值2时,求
有最小值2时,求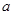 的值;
的值;
(2)当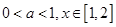 时,有
时,有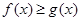 恒成立,求实数
恒成立,求实数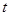 的取值范围.
的取值范围.
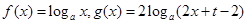
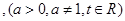 .
.(1)当
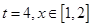 ,且
,且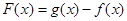 有最小值2时,求
有最小值2时,求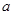 的值;
的值;(2)当
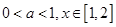 时,有
时,有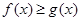 恒成立,求实数
恒成立,求实数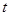 的取值范围.
的取值范围.(1)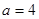 ; (2)
; (2)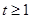 .
.
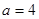 ; (2)
; (2)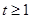 .
.本试题主要是考查了函数的最值,以及不等式的恒成立问题的运用。
(1)利用f(x)分析函数单调性,进而对于参数a分析得到最值。
(2)利用不等式恒成立问题,转换为关于x的不等式,分析参数法得到t的范围。
(1)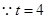 ,
,
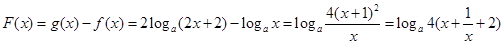
又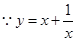 在
在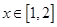 单调递增,
单调递增,
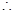 当
当
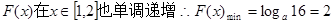 ,解得
,解得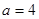
当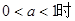
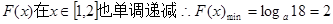 ,
,
解得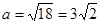 (舍去)
(舍去)
所以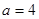
(2)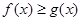 ,即
,即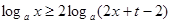
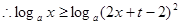
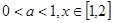 ,
,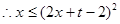 ,
,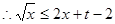 ,
,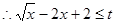 ,
,
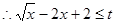 ,依题意有
,依题意有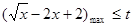
而函数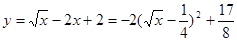
因为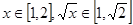 ,
,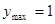 ,所以
,所以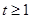 .
.
(1)利用f(x)分析函数单调性,进而对于参数a分析得到最值。
(2)利用不等式恒成立问题,转换为关于x的不等式,分析参数法得到t的范围。
(1)
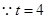 ,
, 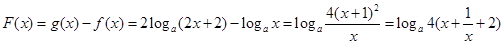
又
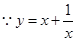 在
在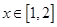 单调递增,
单调递增, 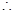 当
当
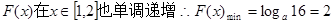 ,解得
,解得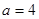
当
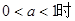
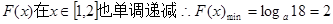 ,
, 解得
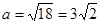 (舍去)
(舍去) 所以
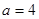
(2)
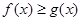 ,即
,即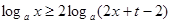
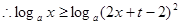
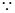
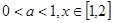 ,
,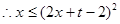 ,
,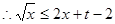 ,
,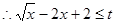 ,
,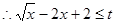 ,依题意有
,依题意有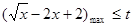
而函数
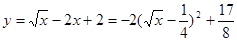
因为
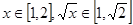 ,
,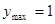 ,所以
,所以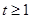 .
.
练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
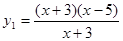 ,
,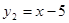
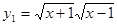 ,
,
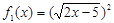 ,
,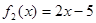
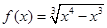 ,
,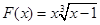
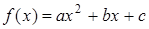 中
中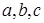 均为实数,且满足
均为实数,且满足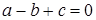 ,对于任意实数
,对于任意实数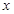 都有
都有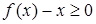 ,并且当
,并且当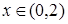 时有
时有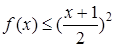 成立。
成立。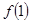 的值;
的值; 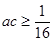 ;
; 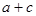 取最小值时,函数
取最小值时,函数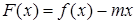 (
(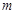 为实数)是单调函数,求证:
为实数)是单调函数,求证: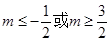 。
。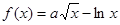
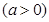
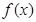 在
在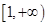 上递增,求
上递增,求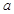 的取值范围;
的取值范围;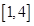 上的最小值.
上的最小值.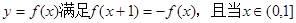 时单调递增,
时单调递增,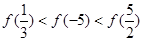
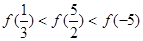
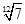 -1
-1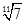 -1
-1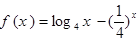 ,
,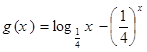 的零点分别为
的零点分别为 ,则( )
,则( )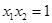
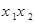 <1
<1