Question

【题目】（本小题满分13分）

如图，在四棱锥中，平面，，，，，，.

（I）求异面直线与所成角的余弦值；

（II）求证：平面；

（II）求直线与平面所成角的正弦值.

Answer 1

【答案】(1) (2)

【解析】试题分析：本小题主要考查两条异面直线所成的角、直线与平面垂直、直线与平面所成的角等基础知识.考查空间想象能力、运算求解能力和推理论证能力.

试题解析：（Ⅰ）如图，由已知AD//BC，故或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC，所以AD⊥PD.在Rt△PDA中，由已知，得，故.

所以，异面直线AP与BC所成角的余弦值为.

（Ⅱ）证明：因为AD⊥平面PDC，直线PD平面PDC，所以AD⊥PD.又因为BC//AD，所以PD⊥BC，又PD⊥PB，所以PD⊥平面PBC.

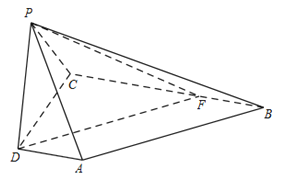
（Ⅲ）过点D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角.

因为PD⊥平面PBC，故PF为DF在平面PBC上的射影，所以为直线DF和平面PBC所成的角.

由于AD//BC，DF//AB，故BF=AD=1，由已知，得CF=BC–BF=2.又AD⊥DC，故BC⊥DC，在Rt△DCF中，可得.

所以，直线AB与平面PBC所成角的正弦值为.