题目内容
13.若函数f(x)=loga(3+3x+4x-m)的值域为R,则m的取值范围为m≥3.分析 若函数f(x)=loga(3+3x+4x-m)的值域为R,是真数可以为任意正数,进而得到答案.
解答 解:t=3+3x+4x-m的值域为(3-m,+∞),
若函数f(x)=loga(3+3x+4x-m)的值域为R,
则3-m≤0,
解得:m≥3,
故答案为:m≥3.
点评 本题考查的知识点是函数的值域,对数函数的图象和性质,难度中档.

练习册系列答案
相关题目
3.设a>1,函数f(x)=loga(a2x-2ax-2),则使f(x)>0的x的取值范围是( )
| A. | (-∞,0) | B. | (-∞,loga3) | C. | (0,+∞) | D. | (loga3,+∞) |
1.已知函数f(x+1)=x2-x,则f(2)=( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
8.已知a、b为实数,命题甲:ab>b2,命题乙:$\frac{1}{b}<\frac{1}{a}<0$,则甲是乙的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | C. | 充要 | D. | 非充分非必要 |
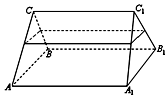 如图,一个三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点.则当底面ABC水平放置时,液面高为( )
如图,一个三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点.则当底面ABC水平放置时,液面高为( )