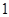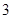题目内容
 ,且
,且 ,则
,则 、
、 的夹角为 ( )
的夹角为 ( )
A. | B. | C. | D. |
C
解析试题分析:因为 ,所以
,所以 ,
,
故 .
.
考点:数量积表示两个向量的夹角;数量积判断两个平面向量的垂直关系.
点评:本题考查利用数量积求向量的夹角,关键是由题意,分析得到| |与
|与 的关系.
的关系.

练习册系列答案
相关题目
过点 作圆
作圆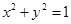 的两条切线
的两条切线 ,
,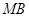
 ,
, 为切点),则
为切点),则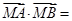 ( )
( )
A.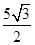 | B.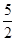 | C.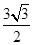 | D. |
已知向量 若
若 与
与 平行,则实数
平行,则实数 的值是
的值是
| A.-2 | B.0 | C.1 | D.2 |
在直角坐标系 中,
中, 分别是与
分别是与 轴,
轴, 轴平行的单位向量,若直角三角形
轴平行的单位向量,若直角三角形 中,
中, ,
, ,则
,则 的可能值有( )
的可能值有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
 ,
, 为平面向量,已知
为平面向量,已知 =(4,3),2
=(4,3),2 +
+ =(3,18),则
=(3,18),则 ,
, 夹角的余弦值等于( )
夹角的余弦值等于( )
A. | B.? | C. | D.? |
 为线段
为线段 上一点,
上一点, 为直线
为直线 外一点,满
外一点,满
 ,
, ,
,  ,
,  则
则 ( )
( )
| A.1 | B. | C. | D.2 |
 |=a,|
|=a,| |=b,则
|=b,则 =
=
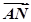 =λ
=λ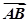 +μ
+μ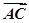 ,则λ+μ的值为 ( )
,则λ+μ的值为 ( )
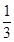

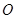 、
、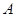 、
、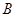 是平面上不共线的三点,向量
是平面上不共线的三点,向量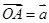 ,
,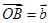 。设
。设 为线段
为线段 垂直平分线上任意一点,向量
垂直平分线上任意一点,向量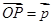 ,若
,若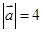 ,
,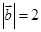 ,则
,则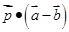 等于
等于