题目内容
 为线段
为线段 上一点,
上一点, 为直线
为直线 外一点,满
外一点,满
 ,
, ,
,  ,
,  则
则 ( )
( )
| A.1 | B. | C. | D.2 |
D
解析试题分析:根据题意可知, 为线段
为线段 上一点,
上一点, 为直线
为直线 外一点,满
外一点,满
 ,
, ,可知和向量的模和差向量的模,同时利用向量数量积的投影的几何意义,可知
,可知和向量的模和差向量的模,同时利用向量数量积的投影的几何意义,可知 在
在 上的投影相等,同时
上的投影相等,同时 ,P,I,C三点共线,又因为
,P,I,C三点共线,又因为 ,可知点I为三角形的内心,那么利用性质可知
,可知点I为三角形的内心,那么利用性质可知 2,故选D.
2,故选D.
考点:向量的加减法,向量的数量积
点评:解决该试题的关键是向量的数量积运用,以及几何意义的准确翻译。属于中档题。尤其是加减法以及数量积的投影的运用。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 ,且
,且 ,则
,则 、
、 的夹角为 ( )
的夹角为 ( )
A. | B. | C. | D. |
已知向量 ,则向量
,则向量 的夹角为 ( )
的夹角为 ( )
A. | B. | C. | D. |
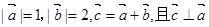 ,则向量
,则向量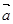 与
与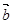 的夹角为( )
的夹角为( )
| A.30° | B.60° | C.120° | D.150° |
设向量 ,
, ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. | B. | C. 与 与 垂直 垂直 | D. ∥ ∥ |
点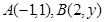 ,向量
,向量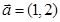 ,若
,若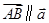 ,则实数
,则实数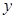 的值为
的值为
| A.5 | B.6 | C.7 | D.8 |
已知 ,O是坐标原点,则
,O是坐标原点,则 等于
等于
A. | B. | C. | D. |
已知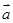 =(-3,2,5),b=(1,x,-1),且
=(-3,2,5),b=(1,x,-1),且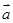 ⊥
⊥ ,则x的值为
,则x的值为
| A.3 | B.4 | C.5 | D.6 |
已知 且
且 与
与 垂直,则实数
垂直,则实数 的值为( )
的值为( )
A. | B. | C. | D. |