题目内容
为如图所示的四块区域涂色，要求相邻区域不能同色，现有3种不同颜色可供选择，则共有________种不同涂色方案（要求用具体数字作答）．
18
分析：本题是一个分步计数问题，首先给左上方一个涂色，有三种结果，再给最左下边的上面的涂色，有两种结果，右上方，如果与左下边的同色，则右方的涂色，有两种结果；右上方，如果与左下边的不同色，则右方的涂色，有1种结果，根据分步计数原理可求．
解答：由题意，首先给左上方一个涂色，有三种结果，
再给最左下边的上面的涂色，有两种结果，
右上方，如果与左下边的同色，则右方的涂色，有两种结果，
右上方，如果与左下边的不同色，则右方的涂色，有1种结果，
∴根据分步计数原理得到共有3×2×（2+1）=18种结果，
故答案为18．
点评：本题考查分步计数原理，本题解题的关键是注意条件中所给的相同的区域不能用相同的颜色，本题是一个基础题．
分析：本题是一个分步计数问题，首先给左上方一个涂色，有三种结果，再给最左下边的上面的涂色，有两种结果，右上方，如果与左下边的同色，则右方的涂色，有两种结果；右上方，如果与左下边的不同色，则右方的涂色，有1种结果，根据分步计数原理可求．
解答：由题意，首先给左上方一个涂色，有三种结果，
再给最左下边的上面的涂色，有两种结果，
右上方，如果与左下边的同色，则右方的涂色，有两种结果，
右上方，如果与左下边的不同色，则右方的涂色，有1种结果，
∴根据分步计数原理得到共有3×2×（2+1）=18种结果，
故答案为18．
点评：本题考查分步计数原理，本题解题的关键是注意条件中所给的相同的区域不能用相同的颜色，本题是一个基础题．
练习册系列答案
相关题目
为如图所示的四块区域涂色，要求相邻区域不能同色，现有3种不同颜色可供选择，则共有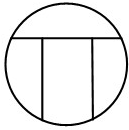
（2009•普陀区二模）园丁要用红、黄、蓝、白四种不同颜色的鲜花布置如图所示圆形花坛的四块区域．要求同一区域内须用同一种颜色的鲜花，相邻区域须用不同颜色的鲜花．设花圃中布置红色鲜花的区域数量为ξ，则随机变量ξ的数学期望Eξ
