题目内容
若方程|x2+4x|=m有实数根,则所有实数根的和可能是( )
| A、-2、-4、-6 |
| B、-4、-5、-6 |
| C、-3、-4、-5 |
| D、-4、-6、-8 |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:函数y=|x2+4x|由函数y=x2+4x的图象纵向对折变换所得,画出函数图象可得函数y=|x2+4x|的图象关于直线x=-2对称,则方程|x2+4x|=m的实根也关于直线x=-2对称,对m的取值分类讨论,最后综合讨论结果,可得答案.
解答:
解:函数y=|x2+4x|由函数y=x2+4x的图象纵向对折变换所得:
如下图所示:
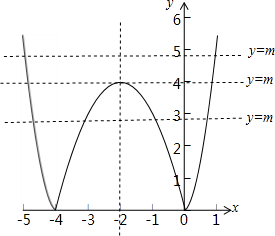
由图可得:函数y=|x2+4x|的图象关于直线x=-2对称,则方程|x2+4x|=m的实根也关于直线x=-2对称,
当m<0时,方程|x2+4x|=m无实根,
当m=0或m>4时,方程|x2+4x|=m有两个实根,它们的和为-4,
当0<m<4时,方程|x2+4x|=m有四个实根,它们的和为-8,
当m=4时,方程|x2+4x|=m有三个实根,它们的和为-6,
故选:D
如下图所示:

由图可得:函数y=|x2+4x|的图象关于直线x=-2对称,则方程|x2+4x|=m的实根也关于直线x=-2对称,
当m<0时,方程|x2+4x|=m无实根,
当m=0或m>4时,方程|x2+4x|=m有两个实根,它们的和为-4,
当0<m<4时,方程|x2+4x|=m有四个实根,它们的和为-8,
当m=4时,方程|x2+4x|=m有三个实根,它们的和为-6,
故选:D
点评:本题考查的知识点是函数的零点与方程根的关系,数形结合是处理此类问题常用的方法.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
如果执行如图的框图,输入N=4,则输出的数S等于( )


A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=ax(a>0,a≠1)满足f(2)=81,则f(
)的值为( )
| 1 |
| 2 |
A、±
| ||
| B、±3 | ||
C、
| ||
| D、3 |
 统计甲、乙两名篮球运动员9场比赛得分情况得到茎叶图如图所示,设甲、乙得分平均数分别为
统计甲、乙两名篮球运动员9场比赛得分情况得到茎叶图如图所示,设甲、乙得分平均数分别为| x甲 |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 运行如图的程序框图,输出的是数列{2n-1}的前7项.若要使输出的结果是数列{3n-1}的前7项,则须将处理框A内的关系式变更为
运行如图的程序框图,输出的是数列{2n-1}的前7项.若要使输出的结果是数列{3n-1}的前7项,则须将处理框A内的关系式变更为