题目内容
(本题满分14分)已知函数 (
( 且
且 ).
).
(Ⅰ)当 时,求证:函数
时,求证:函数 在
在 上单调递
上单调递 增;
增;
(Ⅱ)若函数 有三个零点,求t的值;
有三个零点,求t的值;
(Ⅲ)若存在x1,x2∈[﹣1,1],使得 ,试求a的取值范围.
,试求a的取值范围.
注:e为自然对数的底数。
解:(Ⅰ)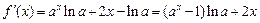 ,
,
由于 ,故当x∈
,故当x∈ 时,lna>0,ax﹣1>0,所以
时,lna>0,ax﹣1>0,所以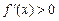 ,
,
故函数 在
在 上单调递增。 ………………………………………4分
上单调递增。 ………………………………………4分
(Ⅱ)当a>0,a≠1时,因为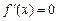 ,且
,且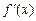 在R上单调递增,
在R上单调递增,
故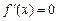 有唯一解x=0。
有唯一解x=0。
要使函数 有三个零点,所以只需方程
有三个零点,所以只需方程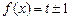 有三个根,
有三个根,
即,只要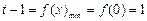 ,解得t=2; ………………………………9分
,解得t=2; ………………………………9分
(Ⅲ)因为存在x1,x2∈[﹣1,1],使得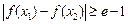 ,
,
所以当x∈[﹣1,1]时, 。
。
由(Ⅱ)知,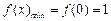 ,
,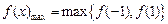 。
。
事实上,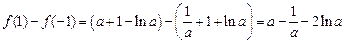 。
。
记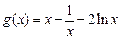 (
(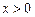 )
)
因为 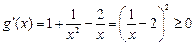
所以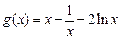 在
在
 上单调递增,又
上单调递增,又 。
。
所以 当 x>1 时,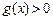 ;
;
当0<x<1 时,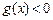 ,
,
也就是当a>1时,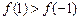 ;
;
当0<a<1时,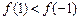 。
。
① 当 时,由
时,由 ,得
,得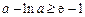 ,
,
解得 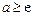 。
。
②当0<a<1时,由 ,得
,得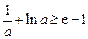 ,
,
解得  。
。
综上知,所求a的取值范围为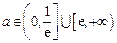 。
。
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 与
与 是定义在
是定义在 上的连续函数,如果
上的连续函数,如果 与
与 仅当
仅当 时的函数值为0,且
时的函数值为0,且 ,那么下列情形不可能出现的是( )
,那么下列情形不可能出现的是( )
A.0是 的极大值,也是 的极大值,也是 的极大值 的极大值 |
B.0是 的极小值,也是 的极小值,也是 的极小值 的极小值 |
C.0是 的极大值,但不是 的极大值,但不是 的极值 的极值 |
D.0是 的极小值,但不是 的极小值,但不是 的极值 的极值 |
 (13分)
(13分)
 上的最大值
上的最大值
 在区间[1,2]上为减函数,求a的取值范围。
在区间[1,2]上为减函数,求a的取值范围。 为函数
为函数
 (
( ,c为常数且1《c《4)的导函数的图象如图所示:
,c为常数且1《c《4)的导函数的图象如图所示:
 1).求
1).求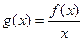 ,求
,求 在
在 上的最大值
上的最大值 。
。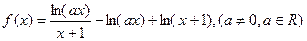 .
.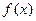 的定义域;
的定义域; 时,若存
时,若存 在使得
在使得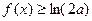 成立,求
成立,求 的取值范围.
的取值范围.
 .
. 在区间[-3,4]
在区间[-3,4] 上的值域
上的值域
 ;
; .若直线
.若直线 1、
1、 的图象以及
的图象以及
 、b、c的值;
、b、c的值; 问是否存在实数m,使得
问是否存在实数m,使得 的图象与
的图象与 的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
 ,
, ,
, 在(0,4)上为单调函数,求
在(0,4)上为单调函数,求 的取值范围.
的取值范围. ).
).