题目内容
把函数的图象y=cos(x+| 4π | 3 |
分析：先根据图象平移的法则推断出图象平移后函数的方程，进而根据原点对称可推断出函数为奇函数，进而求得φ的集合，则|φ|的最小值可得．
解答：解：将函数的图象y=cos(x+
)沿x轴平移|φ|个单位后得到y=cos(x+φ+
)
∵图象关于原点对称
∴cos(-x+φ+
)=-cos(x+φ+
)
∴cosxcos(φ+
)+sinxsin(φ+
)=-cosxcos(φ+
)+sinxsin(φ+
)
∴cos(φ+
)=0∴φ+
=
+kπ
∴φ=-
+kπ，∴当k=1时，|φ|=
最小
故答案为：
| 4π |
| 3 |
| 4π |
| 3 |
∵图象关于原点对称
∴cos(-x+φ+
| 4π |
| 3 |
| 4π |
| 3 |
∴cosxcos(φ+
| 4π |
| 3 |
| 4π |
| 3 |
| 4π |
| 3 |
| 4π |
| 3 |
∴cos(φ+
| 4π |
| 3 |
| 4π |
| 3 |
| π |
| 2 |
∴φ=-
| 5π |
| 6 |
| π |
| 6 |
故答案为：
| π |
| 6 |
点评：本题主要考查了函数y=Asin（ωx+φ）的图象变换，三角函数的奇偶性的应用．考查了学生综合分析问题和解决问题的能力．
练习册系列答案
金钥匙试卷系列答案
相关题目
把函数的图象y=sin（ωx+φ）（ω＞0，|φ|＜
把函数的图象y=sin（ωx+φ）（ω＞0，|φ|＜
）向左平移
个单位，所得曲线的一部分如图所示，则ω+φ=________．
）向左平移
个单位，所得曲线的一部分如图所示，则ω+φ= ．
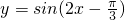的一条对称轴为
；
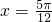的图象向右平移
个单位长度得到y=3sin2x的图象．
；