题目内容
下列结论:
(1)若A,B为两事件,则P(A∪B)=P(A)+P(B);
(2)若A,B为互斥事件,则P(A)+P(B)≤1;
(3)已知一组数据x1,x2,…xn的方差为s2,则2x1+1,2x2+1,…2xn+1的方差为4s2+1;
(4)已知某两个变量x,y具有线性相关关系,且y关于x的回归直线方程为
=0.254x+0.321,则x每增加1个单位,y平均增加0.254个单位.
其中正确命题的个数是( )
(1)若A,B为两事件,则P(A∪B)=P(A)+P(B);
(2)若A,B为互斥事件,则P(A)+P(B)≤1;
(3)已知一组数据x1,x2,…xn的方差为s2,则2x1+1,2x2+1,…2xn+1的方差为4s2+1;
(4)已知某两个变量x,y具有线性相关关系,且y关于x的回归直线方程为
 |
| y |
其中正确命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:阅读型,概率与统计
分析:(1)可考虑A,B互斥时,等式成立,不互斥,显然不成立;(2)由互斥事件的概率公式及概率的基本性质,即可判断;(3)应用方差的性质:若x1,x2,…xn的方差为s2,则ax1+b,ax2+b,…axn+b的方差为a2s2,即可判断;(4)由线性回归直线方程的系数的含义,即可判断.
解答:
解:(1)若A,B为两事件,则P(A∪B)=P(A)+P(B)-P(AB),当A,B互斥时,有P(A∪B)=P(A)+P(B),故(1)错;
(2)若A,B为互斥事件,则P(A)+P(B)=P(A∪B)≤1,故(2)正确;
(3)已知一组数据x1,x2,…xn的方差为s2,则2x1+1,2x2+1,…2xn+1的方差为4S2,故(3)错;
(4)某两个变量x,y具有线性相关关系,且y关于x的回归直线方程为
=0.254x+0.321,则x每增加1个单位,y平均增加0.254个单位,故(4)正确.
故选C.
(2)若A,B为互斥事件,则P(A)+P(B)=P(A∪B)≤1,故(2)正确;
(3)已知一组数据x1,x2,…xn的方差为s2,则2x1+1,2x2+1,…2xn+1的方差为4S2,故(3)错;
(4)某两个变量x,y具有线性相关关系,且y关于x的回归直线方程为
 |
| y |
故选C.
点评:本题主要考查互斥事件的概率的求法,以及方差的性质和线性回归直线方程的特点,是一道基础题.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=n2+
,则( )
| 2 |
| 3 |
| A、an=2n-1 | |||||||
| B、an=2n+1 | |||||||
C、an=
| |||||||
D、an=
|
下列说法正确的是( )
| A、小于90°的角是锐角 |
| B、大于90°的角是钝角 |
| C、0°~90°间的角一定是锐角 |
| D、锐角一定是第一象限的角 |
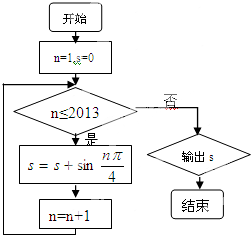
一个算法的程序框图如图,则其输出结果是( )

| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
tan
π的值为( )
| 2 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
工人月工资y(元)依劳动生产率x(千元)变化的回归方程为
=50+60x,下列判断正确的是( )
| ? |
| y |
| A、劳动生产率为1000元时,工资为110元 |
| B、劳动生产率提高1000元,则工资提高60元 |
| C、劳动生产率提高1000元,则工资提高110元 |
| D、当月工资为210元时,劳动生产率为1500元 |